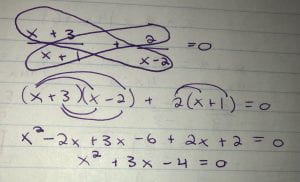Solving Rational Equations 

This week in math we learned how to solve rational equations rather than expressions.

When solving for a rational equation our goal is to determine solution(s) for the variable (x).

If our equation was:

Let’s state the non-permissible values: X cannot be 2, -1, or 0.

Our first step to solving this there is two options; cross multiply or find a common denominator.  You would only be able to cross multiply when the equation includes only two fractions.  In this case, we are able to.

After we cross multiply we need to expand.

After expanding we have to realize whether it is a quadratic or linear equation.  This case it is a quadratic equation.  This means we have to use the zero product law, making one side equal to zero.

Next we have to solve the quadratic, meaning factor it.  This can be done by simply factoring, completing the square, or using the quadratic formula.

After factoring we have found the values for our X variable.  These are our possible solutions and can be checked by verifying them.