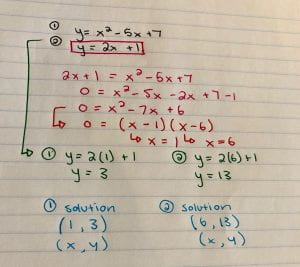Solving Quadratic Systems of Equations Algebraically
This week in math I learned how to solve a quadratic system of equations algebraically.
First, we need to know that a quadratic system is similar to a linear system but what makes it different is that it has a degree of two. Although similarly our end goal is to find the coordinates of the points where each equation intersect with each other.
If my two quadratic equations were:
First I want to get either X or Y by itself. To do this I must rearrange one of the equations. In this case, both are already arranged. I will use the second one because I find it easier to use due to the fact it does not have a square root.
Now that I have Y and is equal to 2x + 1 I will take 2x + 1 and input it into the first equation wherever Y is.
Now I have a quadratic equation that I need to factor.
After factoring I have my X intercepts which are equal to 1 and 6. To find my values of Y I will take each X intercept and use the first equation and replace X with my intercepts 1 and 6 to determine it’s Y partner.
Now you have the partners.
Finally you have your two solutions of coordinates of where the quadratic system intersects.