Top 5 things I learnt in math 10

Write about five things that were most important in your opinion this quarter.

1. Slopes – How to calculate the slope of a line, and create an equation for the slope

The slope is the rise, and run – the horizontal and vertical change between two points, there are three types of equations we learnt about this quarter:

General form ➡ Ax + By + C = 0  ⋅ Point-slope form ➡ m(x – x1) = y – y1  ⋅  Slope y-intercept form ➡ y = mx + b

To calculate slope, you count up (the rise) and across (the run) –

There are four types of slopes – negative, positive, zero, and undefined, these can be identified by “slope guy”

2. Graphing – How to graph points on a graph with an equation

a graph is a diagram that represents data or values in an organized way, the points on the graph represent the relationship between two or more things.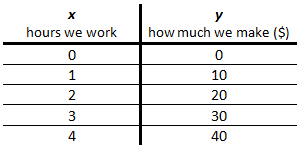

A relation consists of a bunch of ordered pairs and can be drawn as a T-chart this is a great way to organize ordered pairs.

For this, an equation can be made ➡ y = 10x

This is helpful because it is how you figure out points on a graph. It is an equation or rule, where you place the input into the equation to find the output.

3. Trigonometry – How to find missing angles with side lengths and angles including “SOH CAH TOA”

Using this you will be able to find side lengths and angles in a right triangle, when finding the angle, you first need to identify sides and angles already provided in the triangle.

There are three sides – hypotenuse, opposite and adjacent side.

Sin = opposite/hypotenuse   Cos = adjacent/hypotenuse  Tan = opposite/adjacent

Once you identify the sides put your values into the sine equation and solve on a calculator.

4. Functions – How to write an equation in function notation and why it is helpful

Function notation is just another form of an equation for a line on a graph.

Function notation can help you determine and evaluate all the points in your function and place them on the graph, function notation can also be written in other forms such as mapping notation, or as an equation:

f : x —> 2x + 3

Y = 2x + 3

5. Exponents – How to evaluate numbers with exponents as well as exponents in equations

To evaluate expressions with exponents find the base from the exponent, the exponent tells you how many times to multiply the base by itself.

Week 8 math 10

This week in math ten we learnt about the slope of a line and how to find one, we talked about “slope guy” which helps you determine the type of slope.

We learnt about “slope guy”, this helps you remember which lines are positive and negative along with lines that have a slope of zero and an unidentified slope. 

In the week we learnt about linear functions, we practiced determining equations and graphing them. I think the most important thing we learnt was linear equations. 

There are three different types of linear equations we learnt about:

General form ➡ Ax + By + C = 0

Point-slope form ➡ m(x – x1) = y – y1 

Slope y-intercept form ➡ y = mx + b

They can all be used to find the slope of a line, for example, if you are given a set of coordinates (10, 5) and a slope of -2 each equation can help you graph or find other points if you place the given values into the respective places:

[Slope y-intercept form ➡ y = mx + b] – In this equation m represents the slope and b represents the y-intercept so the equation with the given values would look like: y = -2x + 25, the first step would be to place the m value which is -2, then you will need to do some solving to find the “b” value, the coordinates are (10, 5) you place the 10 value in the equation: -2(10) + ___ = y then evaluate, -2(10) = -20, but the number must equal the y value which in this case is 5 so -20 plus what is equal to 5 the answer (25) is your missing value.

[Point-slope form ➡ m(x – x1) = y – y1] – In this equation m represents the slope, x and y represent the coordinates (10, 5) 10 being x and 5 being y, you place thes values into the equation: -2(x – 10) = (y – 5)

[General form ➡ Ax + By + C = 0] – In this equation none of the numbers represent any of the given values (10, 5) as well as -2 the slope, to do this equation you need to start from another equation: use “slope y-intercept form” which in this case is equal to y = -2x + 25 and work backward, one side must equal 0 so you must move the -2x + 25 to the other side of the equation, in doing this the signs reciprocate equaling to y +2x – 25 = 0, now you must reorder the equation: 2x + y – 25 = 0

Week 7 math 10

This week in math 10 we learnt about linear relations and functions. We also talked about relations and t-charts along with intercepts. We learnt about the domain and range as well as how to find them. I think the most important thing we learnt this week was function notation. This is helpful because it is how you figure out points on a graph. Function notation is like an equation or rule, where u place the input into the equation to find the output.

For example, if the questions is: 

f(x) = 2x + 3

And the question is asking for:

f(2)

You will place the x value (2) into the equation:

f(2) = 2(2) + 3, then evaluate:

f(2) = 4 + 3

f(2) = 7

Once you find the answer to the equation you can write these as coordinates:

(2,7) and place them on your graph:

The function notation can help you determine and evaluate all the points in your function and place them on the graph, function notation can also be written in other forms such as mapping notation, or as an equation:

f : x —> 2x + 3

Y = 2x + 3

These are the same as the first example and will give the same answer, but are just written in different forms. 

Week 6 math 10

This week in math 10 we reviewed some grade 9 graphing skills, the most important thing we learnt this week was about relations in graphing.

A relation is a relationship between two sets of information/numbers. X and Y values are linked in an equation they are related, they are a relation.

A relation consists of a bunch of ordered pairs, and can be drawn as a T chart to plot values visual as shown in the example below: 

A relation is when X and Y are connected, every variable produces a different Y value that is dependant on the X value.

This week we leant that in graphing the X axis is always horizontal and the Y axis is vertical, placing a relation on a graph, as shown on the example below plot the X values along the horisontal line and the Y along the vertical line:

In the example above the hours driven is a relation with the distance traveled, the distance depends on the hours so X (hours) is the independent variable and Y (distance) is the dependant variable.

This week in math ten we learnt about multiplying binomials, and polynomials. I think the most important thing we learnt this week was how to draw models when multiplying polynomials, these can be really helpful when you are doing an expression and need a visual way to simplify.

To multiply two polynomials: multiply each term in one polynomial by each term in the other. Once you do that add those answers together and simplify the expression. 

There are several visual ways to multiply a polynomial, you can draw models like an area model, you can also use algebra tiles to draw the expression:

When multiplying polynomials there are also less visual ways to multiply the terms:

Once you have multiplied, you must add like terms, this means combining terms that are the same, like -5x would combine with 8x but not with -4 because they are not like terms.

Knowing how to multiply polynomials by using models is important because you can visually see what you are adding and multiplying.

This week in math 10 we learned about finding angles in right triangles and how they are relevant in everyday life, triangles can be found everywhere and can help you find nights and measurements. Triangles that are not “right triangles” have smaller right triangles inside of them, by using these you can find lengths of other objects. We can determine the sides of one triangle by using the other sides attached to it. 

This can be helpful if you can’t measure something, for example, a tree is very tall and you don’t have the means to measure its high, you can use the shadow of the tree and the angle to find the height of the tree. 

Most phones come with a measuring app, you can use this to find the angle of elevation:

Once you find this, one must measure the shadow of the tree:

When you have found these two thing use “Tangent” to determine the missing side (the height of the tree)

Trigonometry can be used everywhere with everything, to find angles and sides.

Week 3 in math 10

This week in math 10 we learnt about trigonometry, trigonometry figures out lengths between sides and angles of triangles. 

The most important thing we learnt this week was how to find angles, by using the simple acronym; “SohCahToa” 

Using this you will be able to find side lengths and angles in a right triangle. 

When finding the angle, you first need to identify sides and angles already provided in the triangle.

Next, one should label sides – find the hypotenuse, opposite and adjacent side. 

Now using “SohCahToa” sin the side you do have and the side you are looking for and create an equation.

Now solve the equation on a calculator, and you have found your angle or side.

Patterns – Trigonometry consists of patterns, once you know how to do them and continue the patterns you can easily find the angle or side length you are looking for.

This week in math we reviewed, Negative Exponents and Scientific Notation. I think that the negative exponent law is the most important thing we learned this week because once you start doing more advanced problems it is important to know and be knowledgeable about the basics. 

The negative exponent means that the base belongs on the other side of the fraction. 

Step one: Convert the expression into a fraction in the way that any expression can be – by putting it over “1“

Step two: Once the expression is converted into a fraction, use the positive exponents to evaluate or simplify the new expression 

“A negative exponent just means that the base is on the wrong side of the fraction.”

Remember – only move the negative exponents