Top 5 things I learnt in math 10
Write about five things that were most important in your opinion this quarter.
1. Slopes – How to calculate the slope of a line, and create an equation for the slope
The slope is the rise, and run – the horizontal and vertical change between two points, there are three types of equations we learnt about this quarter:
General form ➡ Ax + By + C = 0 ⋅ Point-slope form ➡ m(x – x1) = y – y1 ⋅ Slope y-intercept form ➡ y = mx + b
To calculate slope, you count up (the rise) and across (the run) – 
There are four types of slopes – negative, positive, zero, and undefined, these can be identified by “slope guy”
2. Graphing – How to graph points on a graph with an equation
a graph is a diagram that represents data or values in an organized way, the points on the graph represent the relationship between two or more things.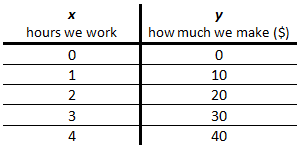 
A relation consists of a bunch of ordered pairs and can be drawn as a T-chart this is a great way to organize ordered pairs.
For this, an equation can be made ➡ y = 10x
This is helpful because it is how you figure out points on a graph. It is an equation or rule, where you place the input into the equation to find the output.
3. Trigonometry – How to find missing angles with side lengths and angles including “SOH CAH TOA”
There are three sides – hypotenuse, opposite and adjacent side.
Sin = opposite/hypotenuse Cos = adjacent/hypotenuse Tan = opposite/adjacent
Once you identify the sides put your values into the sine equation and solve on a calculator.
4. Functions – How to write an equation in function notation and why it is helpful
Function notation is just another form of an equation for a line on a graph.
Function notation can help you determine and evaluate all the points in your function and place them on the graph, function notation can also be written in other forms such as mapping notation, or as an equation:
f : x —> 2x + 3
Y = 2x + 3
5. Exponents – How to evaluate numbers with exponents as well as exponents in equations
To evaluate expressions with exponents find the base from the exponent, the exponent tells you how many times to multiply the base by itself.
| Name | Rule |
|---|---|
| Product law | Add powers together when multiplying bases that are the same – am × an = am+n |
| Quotient law | Subtract powers when dividing bases that are the same – am ÷ an = am-n |
| Power law | Multiply powers together when two exponents are present – (am)n = am⋅n |