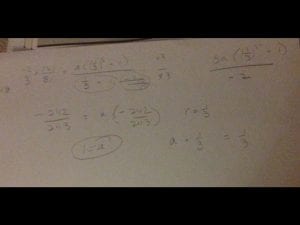This week, I decided I would do my math late at night. Now, I have learned that this is not the best idea. I wanted to get it done and out of the way, however my plans doing it where quickly stopped when I came across a mistake that I made and my brain decided to not work.

After reviewing the question many times I couldn’t find an answer, so I decided to skip it and try it again the next day. Upon seeing it the next day after rest, and my brain working, I realised that the mistake was a simple subtraction mistake in the beginning of the question that threw off the rest of the question. I think this is why it is important to pay attention to your work in the beginning of the question (and throughout the rest of it). I also think it is important to do your math when your brain is working and ready to learn, because this way you are not only less likley to make mistakes, but also are able to learn more from your work and remember how the math works.
This week in pre-calc I learned an important lesson. This has less to do about a particular math problem, or how to solve something, than it is about a question. I think that this is very important for everyone to know. In the past, I have been afraid of asking for help, or questions to teachers when I don’t fully understand something, and wil let it slide, thinking, “I’ll figure it out on my own, and solve it later.” But, I never do really figure out or understand the question, and I let go long enough for the question to become 4 units behind, and to have myself even more confused. I think that this is where I am my own enemy.
So, this week, I didn’t understand some questions, and instead of convicing myself that I would seem stupid, and be judged, and decided to persevire through my stresses, and go get help sooner than later. In doing this, my questions where well explained, I was then able to find the right answer, I felt not stupid at all- the opposite, really, as I had gained more knowledge on how to do the comcept. So, that is why this week, I have no pictures of a specific problem and how I solved it, but rather advice: we judge ourselves much more than others do, and because of this we loose more than gaining what we think will be respect due to a lack of change in judgement from the person we get help from. I hope this helps someone who had the same problem I did, and get the help that they may need.
My mistake this week was a pretty simple lesson to learn, but easy to confuse:

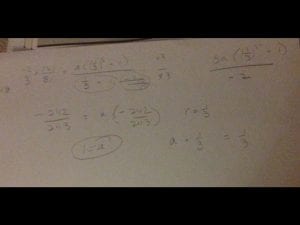
I simply thought I had to multiply the formula used for this question, when I actualyl had to addition this. This is why it is always important to know your formulas and to review your work and ask for help.
Plants:

Cell type: Eukaryotes / Cell number: Multicellular / Feeding type: Heterotrophic

Cell type: Sporophyte / Cell number: Multicellular / Feeding type: Autotroph
Animals:

Cell type: Eukaryotes / Cell number: Unicellular / Feeding type: Heterotroph
- Impala (Aepyceros melampus)

Cell type: Eukaryote / Cell number: Multicellular / Feeding type: Heterotroph (eat grass)
Protists:
Cell type: Eukaryote / Cell number: Unicellular / Feeding type: Heterotroph (eat metazoa, dissolved free amino acids, and bacteria)
- Saprolegnia (Saprolegnia)

Cell type: Eukaryote / Cell number: Unicellular / Feeding type: Heterotroph
Fungi:
- Hygrocybe calyptriformis (Pink Waxcap)

Cell type: Eukaryote / Cell number: Multicellular / Feeding type: Heterotroph
- Hericium coralloides (Coral Tooth)

Cell type: Eukaryote / Cell number: Multicellular / Feeding type: Heterotroph
Archeabacteria:
- Euryarchaeota (Euryarchaeota)
Cell type: Prokaryote / Cell number: Unicellular / Feeding type: Heterotroph
- Lokiarchaeota (Lokiarchaeota)
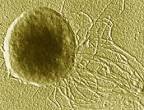
Cell type: Prokarayote / Cell number: Unicellular / Feeding type: Heterotroph
Eubacteria:
- Proteobacteria (Proteobacteria)
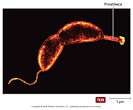
Cell type: Prokaryote / Cell number: Unicellular / Feeding type: Heterotroph
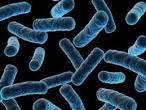
Cell type: Prokaryote / Cell number: Unicellular / Feeding type: Heterotroph
As I was going through the workbook questions for this weekend, I went through all of them learning the methods better as I went. When I started correcting my questions, I came across this answer and didn’t understand why i got it wrong. I thought of many different things that I could have done wrong, but still couldn’t understand why. Then I noticed, that I had made the simplest mistake, and instead of multiplying, I added.
“For each arithmetic series, determine the indicated value.”

I simply didn’t multiply the brackets for 1 + 41(2.5), but I added them instead!
I quickly fixed my error by going re-doing the question – this time being sure to multiply, instead of add! I finished the question, realizing how simple my mistake was to correct.

I will sometimes not correct questions if I cannot figure out what I did wrong, and wait until I can ask someone for help, but I realise now, that if you give yourself enough time to go through the question, and not stress over it too much, you are able to better understand how to do the question (in this case to better understand arethmetic sequences). You are able to leave your studying feeling good about yourself – one of the most important things, so you are motivated to do more, because you realise that you can do it.