Category: Grade 10

Review of Math 10

by nighinar2016

5 Things I learned in Math 10 this year

  1. Practice is key with math. Do the homework to prepare for your tests. Doing the homework will help you be more quick and successful in the unit.
  2. Every unit we did in this class is the foundation to help understand future math courses. Make sure you understand everything.
  3. Finishing your blog posts as soon as possible helps free you from the stress of 11pm Sunday night rush.
  4. Pay attention to all the lessons and take notes. Ask questions!
  5.  Zoning out during a test is problematic.

Week 15 – Slope

by nighinar2016

Slope is the measure of steepness of a line. Slope is the ratio of the vertical change (rise) over the horizontal change (run).

A line segment which rises from left to right has a positive slope.

A line segment which rises from right to left has a negative slope.

The rise is positive if we count up, and negative if we count down.

The run is positive is we count right, and negative is we count left.

A horizontal line segment has a slope of 0.

A vertical line segment has an undefined slope.

The slopes of all line segments on a line are equal.

Slope Formula

m represents slope. Slope Formula is used to find the slope when given two coordinates, without graphing them.

The Formula = 

Example

Find the slope of A(-3, -8) and B(1, 5)

Week 13 – Domain and Range

by nighinar2016

The Domain of a relation is the set of all possible values which can be used for the input of the independent variable (x).

The Range of a relation is the set of all possible values of the output of the dependent variable (y).

The Domain and Range can be found by listing the inputs and outputs.

Ordered pairs

(1,2), (0,5), (3,8), (5,9) (-3,2)

Domain: {-3, 0, 1, 3, 5}

Range: {2, 5, 8, 9}

An Arrow Diagram

D: {2, 4, 6, 8}

R: {1, 3, 5}

Graph

D: {-1, 0, 3, 4}

R: {5, 0, 2, 1}

D: {x E R}

R: {y E R}

D:  {x|-4 ≤ x ≤4, x ∈ R}

D: [-4, 4]

R: {y|0 ≤ y ≤ 5, y ∈ R}

R: [0, 5]

 

Week 12 – Relationship Between Two Quantities

by nighinar2016

A comparison between two sets of elements is called a relation.

Relations can be represented

In Words

“The cost, C, of driving a car is related to the speed, s, at which it is driven.”

A Table of Values

A Set of Ordered Pairs

(20,10)

(30,9.1)

(40,8.4)

A Mapping or Arrow Diagram

An Equation 

C = 0.001s^2 – 0.14s + 12.4

A Graph

Independent Variable represents the inputs

The Corresponding Value – Dependent Variable represents the outputs

In an ordered pair, the values of the first coordinate are the independent values. The value of the second coordinate is therefore the dependent value.

Usually, the first given number in a table of values is the independent value, to the left of above the values of the following number, the dependent value.

In a mapping diagram, the arrows go from the independent value to the dependent value.

In a graph, the horizontal axis (x-axis) has the independent values, and the vertical axis (y-axis)  is the dependent values.

In an equation, usually, the dependent variable is isolated on the left side.

Week 11 – Guidelines for Factoring a Polynomial Expression

by nighinar2016

When factoring a polynomial, there are a couple of steps to take first when trying to factor it.

Always look for the GCF (greatest common factor) before anything else. Checking for a common factor and removing it is the first step. This GCF is for each monomial or the polynomial. When you take it out, place it in-front of the bracket.

For example: 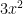3x^2 + 9x^2 – 30

The greatest common factor is 3, because they all share the GCF 3.

3(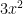x^2 + 3x^2 – 10)

Now, we are either left with a binomial expression or a trinomial expression.

If it is a binomial expression, check to see if there is a difference of squares. Factor as such.

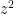z^2 – 1

(z+1)(z-1)

If it is a trinomial expression, 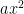ax^2 + bx + c, a either = 1 or does not equal 1.

If a, or the leading coefficient, is a negative number, factor out the negative first.

If a = 1, we can use the method of inspection, finding two numbers that have the sum of the middle term and the product of the last term.

x^2 + 9x + 20

(x + 4)(x + 5)

4 + 5 = 9

4 x 5 = 20

If a does not = 1 and is higher or lower, we can use the method of guess and test or area diagram.

Then check if there is possibility for further factoring, checking to see if there is a difference of squares that can be factored.

We can use an acronym to remember all the steps when factoring polynomials.

CDPEU

Can Divers Pee Easily Underwater

Common factor Difference of squares Pattern Easy Ugly

C – look to see if there is a common factor

D – look to see if there is a difference of squares to factor

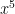P – is it x^2, x, then a number or x^10, x^5, then a number

E – is the leading coefficient 1 and easy to factor by finding two terms that have the sum of the middle term and product of the last.

U – is it an ugly expression that takes more work to find the factoring

Then always check if there is possible further factoring.

Week 10 – Factoring Difference of Squares

by nighinar2016

A difference of squares if a factorization of (a – b)(a + b)

(a – b)(a + b) = a^2 + ab – ba – b^2

= a^2 – b^2

The middle two terms cancel out and you are left with a subtraction of the two terms squared, or a difference of squares.

So, we can apply this distributive property when factoring anything with the same terms but with different signs ( – and + )

Example

(10x – yz)(10x + yz)

Since this follows the rules, we can go straight to

100x^2 – y^2z^2

We can also work backwards with this factorization.

If we have something such as 144p^2q^2 – 4

We know that all those terms are squares.

The first step is to determine if there is a common factor that can be removed. In this case, that common factor is 4.

4(36p^2q^2 – 1)

Now, we are still left with a difference of squares that we can factor.

4(6pq + 1)(6pq – 1)

 

 

Week 9 – Three Important Polynomials Products

by nighinar2016

The distribution of the following polynomials

(a+b)^2 = (a+b)(a+b)

= a^2 + ab + ba + b^2

= a^2 +2ab + b^2

 

(a - b)^2 = (a – b)(a – b)

= a^2 – ab – ba + b^2

= a^2 – 2ab + b^2

 

(a – b)(a + b)

= a^2 + ab – ba – $latex b^24

= a^2 – b^2

When expanding and simplifying a polynomial, we can use the patterns or answers of the following polynomials to help us simplify quicker and easier.

So, when seeing the follow polynomials that fit the equation, you can go straight to the answer without having to go through all the distributive property.

This helps when simplifying longer polynomial expressions.

For example

Expand and simplify (x + 5)(x – 5) – (x + 2)(x+8)

We can go straight from (x + 5)(x – 5)  to  x^2 – 25 because we know that the terms are the same and we know the simplified answer without going through the long distribution.

Now we can continue to simplify the rest. You can’t use any of the three products from above here because (x + 2)(x+8) do not share all the same numbers.

= x^2 – 25 – (x^2 + 8x + 2x + 16)

= x^2 – 25 – (x^2 + 10x + 16)

Bring in the negative.

= x^2 – 25 – x^2 – 10x – 16

The x^2 cancels out because there is a negative and a positive one of the same thing. Continue simplifying and adding like terms.

= -10x – 41

–

I found this lesson very useful. It was easy to remember once I got the hang of it and it helped me simplify polynomials quicker.

Week 8 – F.O.I.L

by nighinar2016

When multiplying two binomials, we can use a distributive property called F.O.I.L.

The distributive property for binomials: (a+b)(c+d) = a(c+d) +b(c+d) = ac + ad + bc + bd

Instead of going through the distributive property individually, we can use the simplified way, the F.O.I.L method.

The acronym:

F – first term in each bracket – ac

O – outside terms – ad

I – inside terms – bc

L – last term in each bracket – bd

Example:

–

A challenge with F.O.I.L is that it can become confusing if you forget what you have multiplied and what you haven’t. Writing down the arrows as you go can be very helpful and help you know where you are at and how much you have left.