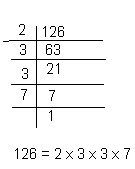week 8 in math 10
this week in math 10 I learned how to check that my answers are correct when solving a triangle, so I know that 90⁰ is greater that 45⁰ which is greater than 1⁰, also to remember that the angles in a triangle add up to 180, if my triangle looks like this after ive attempted to solve it:
i need to make sure that angle B is greater than A which is bigger than C, because angleB represents 90 degrees which has to be the largest, angle A represents 60 degrees which would be the second largest, it is between 89 and 45. and angle C would be the smallest because its 30 degrees, between 45 and 1. then the side lengths across from those angles also have to be greatest to smallest in that order. 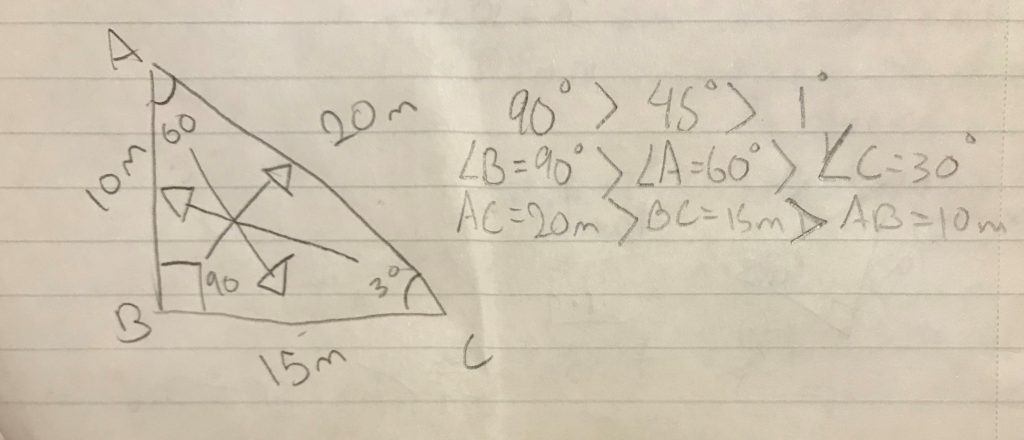
week 7 in math 10
this week in math 10 we started our unit on trigonometry. I learned how to use my calculator to calculate the side lengths of triangles using sine, cosine and tangent. I also learned that you can also calculate the angles ex if sinB= 12/30, where B is the angle, to find the angle you put and get 23.57812….rounded to the nearest whole number = 24 degrees. I also learned how that works, so we have sinB=o.4 and we have to isolate B so we divide each side by sin
which equals
. now we have to move
to the top of the fraction so it becomes
because the exponent of 1 now becomes negative. then you punch
into a calculator to find B
would look something like this:
week 6 in math 10
this past week in math 10 I learned that you can calculate the volume of a prism by taking the volume of a pyramid with the same height and bottom, and multiplying it by 3. this also works to find the volume of a pyramid by taking the volume of a prism with the same height and bottom, and dividing it by 3. from this I learned that formula for the volume of a pyramid is the area of the base, multiplied by the height, all divided by 3 or multiplied by
week 5 in math 10
this week in math 10 we started our unit on measurement. we went over conversions in the metric system and imperial. At first I did not understand how to do this at all but with some practice and a little help I am starting to understand it way more. we also did some work on surface area and volume, Ms Burton showed us how to write out everything you are thinking step by step, I found this helpful because it kept me from losing track of numbers and getting lost in the question.
week 4 in math 10
this week in math 10 I learned about scientific notation, it is basically how you can turn a large number ex. 34500000000.00 into a simple expression that is easy to work with. we have “a” needs to be greater than 1 and less than 10. “n” just represents the unknown exponent. so to find “a” we need to move the decimal from 34500000000.00 so the number follows the rules of “a”. it becomes 3.45 because 3.45 is greater than 1 and less than 10. now the decimal “n” becomes the number of times we moved the decimal over so n=10 and the expression becomes
now if the number were to be 0.000000345 same rules apply only the exponent will be negative because you are moving the decimal to the right this time the expression would be
Week 3 in math 10
this week in math 10 i learned and reveiwed exponents, focusing on the laws, i learned that you can use them in any order to solve a problem involving combining the laws. For example in this expression:
It is the same expression in both pictrues, in the first picture i did the multiplication law, power of a power then division. In the second photo i did power of a power, multiplication then divison and both attempts had the same answer outcome.
Week 2 in math
Throughout this past week i have learned more about prime factorization. Speciffically how to demonstrate prime factorization, you can use one of two ways. You could use a factor tree (first picture) or a divison table (second picture) to find out the prime factorization. For both methods you start with the lowest prime factor, and divide it into the example number. Then you continue to do the same thing with that number untill it no longer factors perfectly, then you take the next lowest prime number that factors and the rule continues on. I prefer to use division tables becasue with especially largr numbers, in factor trees the work can get sloppy and confusing.