1: represent repeated multiplication with exponents:
An example of repeated multplication would be writing/expanding out as (2)(2)(2)(2) or 2x2x2x2 or 2•2•2•2
2. Describe how powers represent repeated multplication:
Poweres represent repeated multiplication by showing that ex. (5)(5)(5)(5) would be written as because it’s saying multiply 5 by 5, 4 times. The exponent is 4 because thats how many times your multiplying the base, which is 5. The exponent is the small number and the base is the larger number. So
= (5)(5)(5)(5)
3. Demonstrate the difference between the exponent and the base:
in a power, there’s an exponent and a base, a little number and a larger number. The little number is the exponent and the larger number is the base. The base is multiplied by itself as many times as the exponent. So if the base is 5 and the exponent is 3, then 5 multiplies by itself 3 times. (5)(5)(5) =
4. Demonstrate the difference between two givin powers in which the exponent and the base are interchanged by using repeated multiplication:
=
so this means that is different than
.
means you multiply 2 by itself 3 times, so, (2)(2)(2) because the base is 2, and the exponent is 3, and you multiply the base by itself as many times as the exponent tells you to.
means multiply 3 by itself twice. So (3)(3) so these are two completely different answers.
= 8 and
= 9. They do not equal the same answer even though they both use the same numbers.
5. Evaluate powers with integral bases (excluding base 0) and whole number exponents:
ex. = 125
ex. = 81
ex. = 32
6. Explain the role of parentheses in powers by evaluating a given set of numbers such as ,
and
:
so means (-2)(-2)(-2)(-2) = +16
means (-1)(2)(2)(2)(2) = (-16)
means (-1)(2)(2)(2)(2) = (-16)
7.explain the exponent law for multiplying and dividing powers with the same base:
law for dividing: ex. , you would subtract the exponents while keeping the base as it is so it becomes
wich equals to
= 16
law for multiplying: ex. , you would add the exponents while keeping the base as it is so it becomes
which equals to
= 32
8. Explain the exponent laws for raising a product and quotient to an exponent:
raising product to an exponent would be you would multiply the exponents, you multiply because like any other equation, if there’s a bracketed number next to another number it means multiply ex. 2(5) just means 2×5 = 10. And you multiply the exponents because it follows pemdas or bedmas.so..
=
=
= 15,625
raising quotient to an exponent is the same as dividing same base powers, you subtract the exponents. So over
=
=
= 25
9. Explain the law for powers with an exponent of 0:
anything to the power of 0 = 1
10. Use patterns to show that a power with an exponent of zero is equal to one:
When the power decreases, the answer divides by it’s base. Ex = 32
, to find the answer you can take 32 from
And divide it by the base to get the answer for
= 16 this means you would divide 32 by 2(base) to get 16
same with to get the answer you can divide 16 by 2 = 8
= 8
= 8/2 = 4.
= 4
= 4/2 = 2.
= 2
then to get , you continue on the rule, you find the answer for
Which is 2 and divide it by the base which is 2 in this case. So
= 2/2 = 1.
= 1
11. Explain the law for powers with negative exponents:
the law for negative exponents is the same for any base except zero. If the base is raised to a negative exponent, you must reciprocal the base so then the exponent becomes positive. Ex. over 5, you would change it so 5 is now over 2, which makes the exponents positive. Then you complete the equation, in this case you would do
= 25. Then divide the numerator by the the denominator so 25/2=12.5
12. Use patterns to explain the negative exponent law:
For example you would reciprocal the base. It becomes
over 2, then you just solve it how you normally would. It becomes 1 over 3 because before, it was just 3 and 3=3 over 1
13.
I can apply the exponent laws to powers with both inegral and variable bases:
when solving powers with variables as bases, you always follow the same rules as if the base were a number but you may not be able to solve the equation completely
ex. =
there is no different ce between the power and the answer because it can’t be solved any further.
ex. x
=
This is the final answer because you can’t multiply Y by itself 7 times and get an answer further than this answer.
ex. divided by
=
This is the final answer because you can’t multiply N by itself twice and get an sneer further than this answer.
14. I can identify the error in a simplification of an expression involving powers:
I will spot the error in the equation below and correct it-
=
this answer is wrong.
=
=
15. Use order of operations on expressions with powers:
when following the order of operations with powers, we always use bedmas.
ex. x
= 2x2x2x2 = 16, 4x4x4 = 64, 16×64=1024
Ex. 2 =
= 4×4= 16. 2×16= 32
16. Determine the sum and difference of two powers:
adding powers ex. = (4x4x4) + (2x2x2x2x2) = 64+32= 96
subtracting powers ex. = (3x3x3) – (6×6) = 27-36= -9
17. Identify the error in applying the order of operations in an incorrect solution:
3 =
this is wrong because with order of operations, you always do the exponent before you multiply.
3 = 6x6x6 = 216. 216 x 3 = 648
18. Use powers to solve measurement problems:
Imagine a shaded square with each side 5cm, and a smaller, white square with each side 2cm sitting inside the shaded square. how do you find the area of the shaded part? Well Area=LxW, because we are talking about perfect squares, LxW is the same as saying To the power of 2. for the larger square so = 25. Then the smaller white square,
= 4. So to find the shaded part you subtract them, 25- 4 = 21. Area of the shaded part =
19. Use powers to solve growth problems:
Ex. There are 20 people at a concert. The amount of people doubles ech hour, how any people will there be in ____ hours?
2 hours?
20 x = 20 x 4= 80 people. In 2 hours there will be 80 people
4 hours?
20 x = 20 x 16 = 320 people in 4 hours
6 hours?
20 x = 20 x 64 = 1280 people in 6 hours
etc.
20. Applying the order of operations on expressions with powers involving negative exponents and variable bases:
A power involving a variable base with a negative exponent would be:
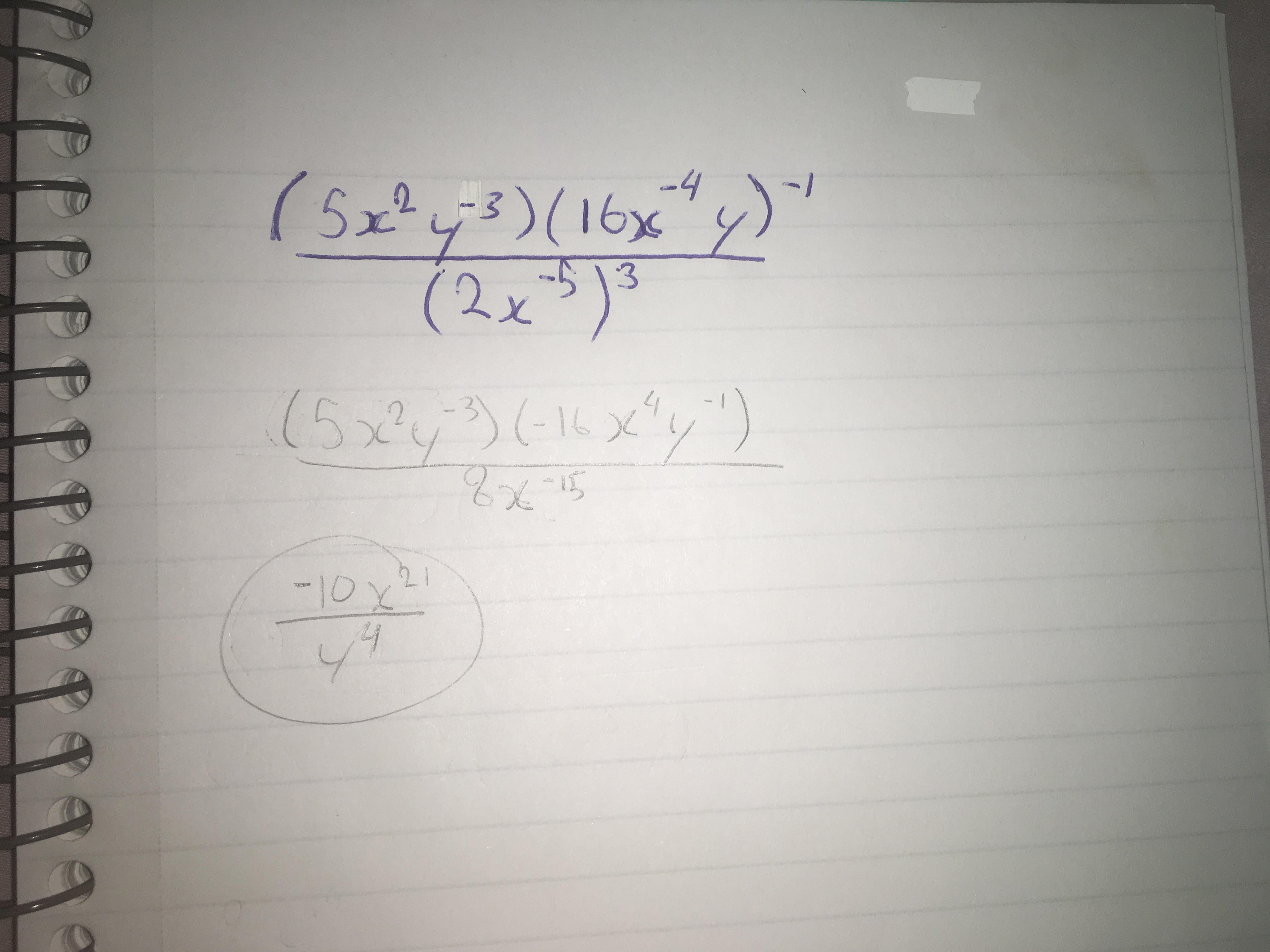
1) You did a good job on labeling all of your learning outcomes. Great job it looks nice as it is finished!
2) Your explanations are very clear and easy to understand. You have done a good job in explaining the learning outcomes and they are all detailed, but not overly detailed.
3) On question five you had made a calculation mistake by writing 3³=81 when it actually equals 27. Also for question 12, you wrote “3 over 1”. Which at the end means just 3 and you probably actually meant 1 over 3.
4) Overall, the way you have it all organized makes it very easy to read and understand. You also have added images and multiple examples to try to get your point across. You also have done a good job with your coding and it makes it look very neat!
5) Some things you could have improved are that you could have coded your fractions. It’s a bit hard to understand when you are using brackets to show fractions and words to show fractions. Also for question 20, after you had simplified it, I can’t tell what number the coefficient in the denominator is. You have some spelling mistakes to so maybe it you re-read it they could have been eliminated. But at the end it looks good! Great job Morgan! ^-^
Hi Morgan,
You still need a parent comment.
I have looked over your math homework and overall i think that you did a good job. I do think there are a few areas where you could go into more detail, such as in question 3, I think you could explain the difference between the exponent and the base in better detail. You said that the exponent is the small number in the power and I was confused in what that meant. As in the exponent is the small number meaning in numerical form or the actual font size.
Thanks Morgan, Please check your OneNote for specific feedback.