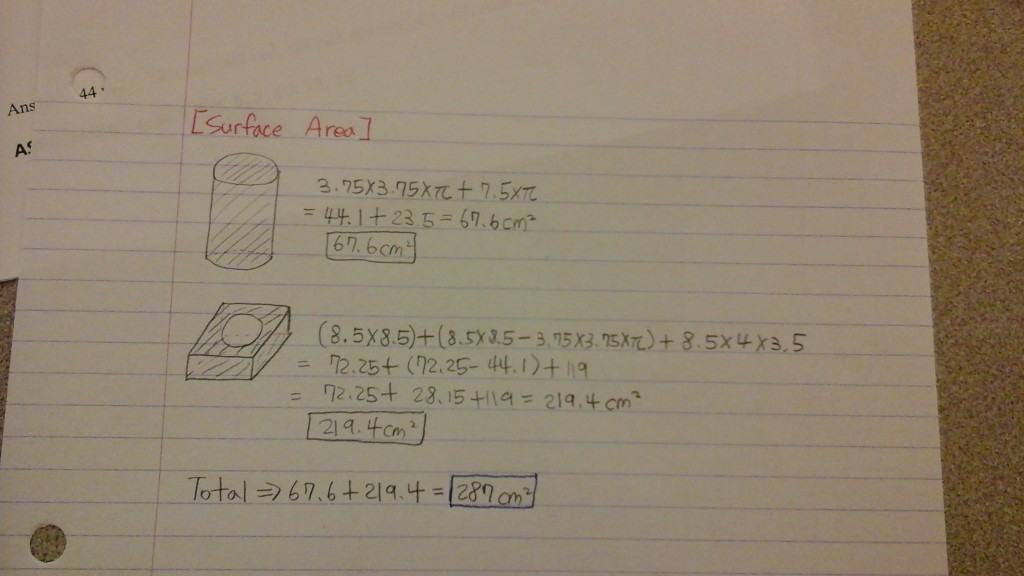Grade 9
Imapct on First Nations Persuasive Essay
Essay outline : essay_outline-impact_on_first_nations_2016
Essay :ESSAY
Everything I know about exponents
1) Represent repeated multiplication with exponents
2×2×2 = 2^3
2) Describe how powers represent repeated multiplication
3×3×3×3 – The base is 3 and the exponent is the number of 3’s it has. So 3×3×3×3 is 3^4.
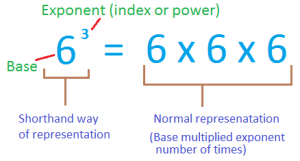
3)Demonstrate the difference between the exponent and the base by building models of a
given power, such as 3 2 and 2 3 .
3^2 : The base is 3 and the exponent is 2
2^3 : The base is 2 and the exponent is 3.
4) Demonstrate the difference between two given powers in which the exponent and the base
are interchanged by using repeated multiplication, such as 3 2 and 2 3 .
3^2 equals to 3×3 and 2^3 equals to2×2×2
5) Evaluate powers with integral bases (excluding base 0) and whole number exponents.
5^2 = 25
6) Explain the role of parentheses in powers by evaluating a given set of powers such as (-2)^4, (-2^4) and -2^4
(-2)^4 = (-2)×(-2)×(-2)×(-2) = 16 (-2^4) = -2×2×2×2 = -16 -2^4 = -2×2×2×2 = -16
7) Explain the exponent laws for multiplying and dividing powers with the same base.
Multiplying powers with the same base : add the exponents
Dividing powers with the same base : subtract the exponents
8) Explain the exponent laws for raising a product and quotient to an exponent.
Product : Keep the base, add the exponents, and if there is a coefficients multiply them.
Quotient : Keep the base, add the exponents, and if there is a coefficients divide them.
If the two bases are different, you divide the bases and subtract the exponents.
9) Explain the law for powers with an exponent of zero.
Whenever the exponent is a zero, the answer is 1.
10) Use patterns to show that a power with an exponent of zero is equal to one.
2^3 = 8 2^2 = 4 2^1 = 2 2^0 = 1
11) I can apply the laws of exponents.
ex) 2^3× 2^9= 2^12
3^5 ÷ 3^2=3^2
(2^3)4=2^12
5^0=1
12) I can identify the error in a simplification of an expression involving powers.
If I know the exponent law corectly, I can identify the error.
ex) 2^3 × 2^4 = 2^12 The answer is wrong because it multiplied the exponents. You have to add the exponents. So the answer is 2^7
13) Use the order of operations on expressions with powers.
To evaluate expressions wig powers in which you have to use BEDMAS.
First you do the brackets first, and if there is a multiplication or a division u have to do that first than addition and subtraction.
ex) (2+3×4) + 2^2= (2+12) + 4=14+4=18
14) Determine the sum and difference of two powers.
Sum : 3^2 + 3^3 = 9 + 27 = 36
Difference : 5^2 – 5^1 =25 – 5= 20
15) Identify the error in applying the order of operations in an incorrect solution.
Wrong way : 3 ×2 + 2^4 correct way : 3×2 + 2^4
= 3 × 18 = 54 =6 + 16=22
17) Use powers to solve problems (growth problems)
Ex) I get 5 dollars a month. How much money do I get after 3months?
1 month : 5 dollars
2 month : 10 dollars (5^2)
3 month : 15 dollars (5^3)
18) Solve problems by applying the order of operations.
Ex) I bought two red pens that each costs 2 dollars and a high liter that costs 1 dollar. 2×2 + 1 = 4+1=5