This week we learnt how to multiply polynomials when there’s more than two parts to the equation.

Here’s an example of an equation you might do: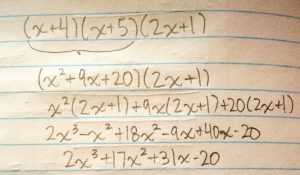

You might receive an equation that looks like this: (2x+3)(-x+6)+(3x+x-4). To simplify the equation, here’s what you do:

First, you have to simplify the first two parts which, in the example above is (2x+3)(-x+6). You can either use an area diagram or figure it out algebraically.

In this case, I’m going to do it algebraically. So, you write out the entire equation and continue from there.

[(2x+3)(-x+6)](3x+x-4)

= [2x(-x+6)+3(-x+6)](3x+x-4)

The first thing you do is simplify the part of the equation in the square brackets.

=[(2-2+12x)+(3-3x+18)](3x+x-4)

=[2++9x+18](3x+x-4)

Next, you simplify the part that’s in the square brackets with the part that is outside of those brackets algebraically.

=3x(2++9x+18)+x(2++9x+18)-4(2++9x+18)

= (6+3+27+54x)+(2++9+18x)-(8-4-36x-72)

Finally, you simplify it all together to make a shorter equation.

= (8-4+32+36x-72)