In Chapter 6, I learned about Factoring polynomial expressions.
In lesson 1, we reviewed how to expand a fraction and what the Greatest Common Factor (GCF) is and how to find it using prime factorization. I learned to factor a polynomial by removing the greatest common factor.
In lesson 2, I learned that sometimes the GCF is a binomial instead of a monomial, this is called Binomial Common Factors. This is used when factoring by grouping, by removing the GCf from a pair of terms and then factoring by a binomial common factor. We also learned about Monomial Common Factors involving fractions and when to use them (in later lessons and math courses).
Lesson 3 started with algebraic tile diagrams and how to use them to write polynomial expressions, then factor trinomials. I also learned to factor trinomials without algebra tiles, and by inspection by expanding the equation and inspecting to solve. Furthermore, I learned that in some situations the expression cannot be factored.
In Lesson 4, I learned how to factor trinomials of the form X² +bx +c. In order to factor this, there needs to be two integers whose product is equal to C and whose sum is equal to B. If this isn’t possible, then I know that the expression cannot be factored. If the product is positive, then the two integers have the same sign (both positive, or both negative). If the product is negative, then one of the integers is positive.
 Lesson 5 introduced Difference of Squares. (Shown in image) This is a method to factor an expression described as: a² – b² = (a-b)(a+b).
Lesson 5 introduced Difference of Squares. (Shown in image) This is a method to factor an expression described as: a² – b² = (a-b)(a+b).
In Lesson 6 I learned a method for factoring polynomials that took the form of ax² + bx + c, this method is called decomposition. “The method of factoring ax² + bx + c, by splitting the value of b into two integers whose product is ac and whose sum is b.” Is how the textbook described the decomposition method. This method can also be used to factor trinomials with the form ax² + bxy + cy².
In lesson 7 we reviewed what perfect squares were and how we use them in factoring. When a trinomial is a perfect square, the middle term has to be twice the product of the square roots of the first and last term. Using this rule, we identified which polynomials were considered perfect squares and factored. We also expanded on the previous methods of factoring.
Lesson 8 was just a review and guidelines of factoring.
The following breakdown/reivew was included in the textbook.
- Look for a common factor. If there is one, take out the common factor and look for further factoring.
- If there is a binomial expression, look for a difference of squares.
- If there is a trinomial expression of the form x² + bx + c, look for factoring by inspection.
- If there is a trinomial expression of the form ax² + bx + c, look for factoring using decomposition. Watch out for perfect square trinomials.
- If there is a polynomial with four terms, look for factoring by grouping.
- After factoring, check to see if further factoring is possible.
Lesson 9 was an enrichment lesson on solving polynomial equations in which the left side is a polynomial expression and the right side is equal to zero.
 Lesson 1 was review and a preview into the chapter. We reviewed what a variable and what an algebraic expression is. We also learned the difference between a monomial, binomial, trinomial, and a polynomial. (shown in image). With these polynomials, you can classify them by degree. “The degree of a monomial is the sum of the exponents of its variable(s)” and “the degree of a polynomial is the degree of the term with the highest degree.” After we learned how degrees work, we started to add and subtract polynomials. At first, with algebra tiles, then, just algebraically.
Lesson 1 was review and a preview into the chapter. We reviewed what a variable and what an algebraic expression is. We also learned the difference between a monomial, binomial, trinomial, and a polynomial. (shown in image). With these polynomials, you can classify them by degree. “The degree of a monomial is the sum of the exponents of its variable(s)” and “the degree of a polynomial is the degree of the term with the highest degree.” After we learned how degrees work, we started to add and subtract polynomials. At first, with algebra tiles, then, just algebraically.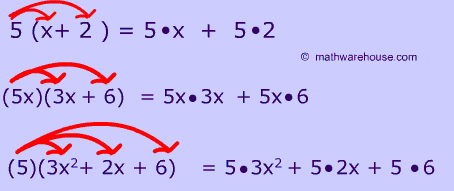 In lesson 3, We expanded on what we knew and learned how to multiply two binomials together. In this lesson, there were two models, algebra tiles and an area diagram, however I prefer to solve algebraically. Again, we expanded on the distributive property concept. The distributive property for two binomials is as follows: (a+b)(c+d) = a (c+d) b (c+d)= ac +ad +bc +bd.
In lesson 3, We expanded on what we knew and learned how to multiply two binomials together. In this lesson, there were two models, algebra tiles and an area diagram, however I prefer to solve algebraically. Again, we expanded on the distributive property concept. The distributive property for two binomials is as follows: (a+b)(c+d) = a (c+d) b (c+d)= ac +ad +bc +bd.