In Chapter 2, I learned all about exponents 🙂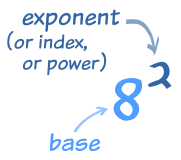 
In the first lesson I learned all about powers with whole number exponents, and what the base, exponent and index is.
In lesson two, I learned about the exponent laws. When multiplying exponents (with same base), add the exponents together. When there is a power raised to a power, multiply the exponents. And when dividing powers, subtract the exponents.
Lesson three, I learned about Integral exponents. When a base is raised to a negative exponent, you transfer the negative exponents into a fraction with a positive exponent.
The next lesson we did was lesson five, which taught us about rational exponents. We learned about fractions in radical form and methods on how to evaluate and simplify them. We continued this learning into lesson six, where we took bases raised to fraction exponents and wrote them in radical form, and simplified.
Using a method called “Euclid’s Algorithm” I will find the LCM and GCF of the numbers 425 and 187. First, let’s find the GCF, and then using that we can find the LCM.
First, divide the two numbers (the first number by the second number). 425 / 187 = 2 with a remainder of 51. From this, we can draw the conclusion that 425= 2 x 187 + 51
Next, divide the second number (187) and the remainder (51). 187 / 51 = 3 R 34. We can draw the conclusion that 187 =3 x 51+34.
Take the last part of the equation, (the first remainder, 51, and the second remainder, 34,) and divide those two together. Keep on doing this until you get a remainder of zero.
51/34= 1R 17 so 51= 1 x 34 +17
34/17= 2R 0 so 34= 2 x 17 + 0
So the GCF is 17.
Â
To find the lowest common multiple, multiply the two original numbers.
425 x 187 = 79, 475
Then divide that by the GCF that we just found.
79, 475 / 17 = 4,675
The lowest common multiple of 425 and 187 is 4,675.
Â
I prefer prime factorization, because with this method you need to find or be given the GCF first. Finding the GCF is difficult because it can get confusing when dealing with remainders and lots of equations. Finding the lowest common multiple is a lot easier because you just have to divide two numbers but finding the GCF is more complicated than just using the prime factorizations method.