Posts Tagged ‘10’

Narrative Essay Corrections
Two things I did well:
- I made my voice clear throughout the essay and writing.
- The writing represented me, my personality came through.
Two things I would improve:
- Dialogue!
- Just grammar tweaks and mistakes.
IMPORTANT: Sometimes edublog erases the high quality of a picture when it is inserted into a post, if that happens please click on the graph (picture) for it to appear in a new tab with higher quality so you can actually read it!!!

Name: Mara BLK: D
CHALLENGE: Make a boat that can float in water and hold the most amount of pennies.
PROBLEM: What materials can we use and how can we make a boat that will float in water?
HYPOTHESIS: If we use tinfoil as a base, and attach the straws on the perimeter and marshmallows on the corners of the bottom, the boat should be able to float.
IDEA FOR ORIGINAL DESIGN: Insert image and write a description explaining your thinking/reasoning as to why you chose that particular design



We thought that the straws would add some support to the base, and the marshmallows would be able to resist water and therefore assist the boat in staying above the water once weight (pennies) were added. We also decided to add wax paper in the middle to hold a sort of curve for the pennies.
HOW MANY PENNIES DID YOUR BOAT HOLD?
35
WHAT WOULD YOU KEEP OR CHANGE ON YOUR BOAT DESIGN IF YOU WERE TO DO THIS AGAIN? (saying nothing is not an option)
For the most part, our theory worked. The straws added support to the base and but it also allowed some water to seep through, next time, we should make sure that the ends of the straws are secure so they become more water resistant. The marshmallows also really helped the boat stay afloat and so did the wax paper, however it could only hold 35 pennies.
In Chapter 5, I learned about Polynomial Operations
 Lesson 1 was review and a preview into the chapter. We reviewed what a variable and what an algebraic expression is. We also learned the difference between a monomial, binomial, trinomial, and a polynomial. (shown in image). With these polynomials, you can classify them by degree. “The degree of a monomial is the sum of the exponents of its variable(s)” and “the degree of a polynomial is the degree of the term with the highest degree.” After we learned how degrees work, we started to add and subtract polynomials. At first, with algebra tiles, then, just algebraically.
Lesson 1 was review and a preview into the chapter. We reviewed what a variable and what an algebraic expression is. We also learned the difference between a monomial, binomial, trinomial, and a polynomial. (shown in image). With these polynomials, you can classify them by degree. “The degree of a monomial is the sum of the exponents of its variable(s)” and “the degree of a polynomial is the degree of the term with the highest degree.” After we learned how degrees work, we started to add and subtract polynomials. At first, with algebra tiles, then, just algebraically.
Lesson 2 taught us how to multiply a polynomial by a monomial. Again, we used algebra tiles at first but then we learned how to expand an expression using the distributive property. The distributive property is a(b+c) = ab +ac. (examples shown in image below).
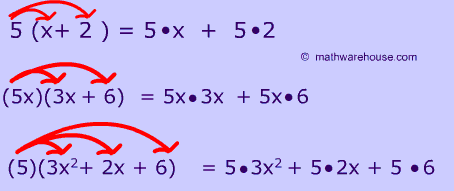 In lesson 3, We expanded on what we knew and learned how to multiply two binomials together. In this lesson, there were two models, algebra tiles and an area diagram, however I prefer to solve algebraically. Again, we expanded on the distributive property concept. The distributive property for two binomials is as follows: (a+b)(c+d) = a (c+d) b (c+d)= ac +ad +bc +bd.
In lesson 3, We expanded on what we knew and learned how to multiply two binomials together. In this lesson, there were two models, algebra tiles and an area diagram, however I prefer to solve algebraically. Again, we expanded on the distributive property concept. The distributive property for two binomials is as follows: (a+b)(c+d) = a (c+d) b (c+d)= ac +ad +bc +bd.
I learned to use the acronym FOIL to help remember which terms to multiply first
F- First term in each bracket
O- Outside terms
I- Inside terms
L- Last terms in each bracket
In lesson 4, we practised the FOIL method and multiplied polynomials together. This continued in Lesson 5, and we were introduced problem solving by multiplication of polynomials and went more in depth with this in lesson 6.
In Chapter 4 I learned about Trigonometry.
In lesson 1, I learned about the Trigonometric Ratios. The three ratios are Sine (opposite over hypotenuse), Cosine (adjacent over hypotenuse), and Tangent (opposite over adjacent). I also learned about SOH COH TOA, and what it means. SOH represents the sine ratio, COH represents the cosine ratio, and TOA represents the tangent ratio.
In lesson 2, I learned how to use a calculator to solve trig ratios. When given the ratio, I need to find the angle and vice versa, to do this we use the inverse operations of said ratio.
In lesson 3, I learned how to calculate the length of a side in a right triangle and how to cross multiply to solve.
In lesson 4, I learned how to calculate the measure of an 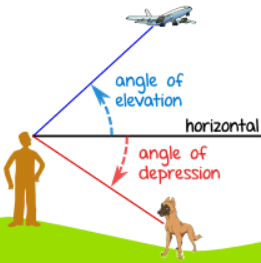 angle in a right triangle. In order to do this, you need to know at least two side lengths of the triangle. And then you use a trig ratio (SOH CAH TOA) and plug in the numbers to solve. I also learned about the angle of elevation and the angle of depression. (Image shown). The angle of elevation is measured upwards from the horizontal line, while the angle of depression is measured downwards from the horizontal line. I learned how to apply this knowledge to solve word problems.
angle in a right triangle. In order to do this, you need to know at least two side lengths of the triangle. And then you use a trig ratio (SOH CAH TOA) and plug in the numbers to solve. I also learned about the angle of elevation and the angle of depression. (Image shown). The angle of elevation is measured upwards from the horizontal line, while the angle of depression is measured downwards from the horizontal line. I learned how to apply this knowledge to solve word problems.
In lesson 5, we reviewed and practised solving right triangles. Depending on the information that was given for each example, we used the Pythagorean Theorem, Trig, or both.
In lesson 6, problem solving was introduced and I learned how to solve them using the trigonometric ratios. I also learned about Bearings which are angles measured clockwise from the north direction and they were also included in the word problems.
And lastly, lesson 7 was more practice and problem solving using trig ratios. These questions were little more complicated and we started solving problems with three dimensional shapes.
Using a method called “Euclid’s Algorithm” I will find the LCM and GCF of the numbers 425 and 187. First, let’s find the GCF, and then using that we can find the LCM.
First, divide the two numbers (the first number by the second number). 425 / 187 = 2 with a remainder of 51. From this, we can draw the conclusion that 425= 2 x 187 + 51
Next, divide the second number (187) and the remainder (51). 187 / 51 = 3 R 34. We can draw the conclusion that 187 =3 x 51+34.
Take the last part of the equation, (the first remainder, 51, and the second remainder, 34,) and divide those two together. Keep on doing this until you get a remainder of zero.
51/34= 1R 17 so 51= 1 x 34 +17
34/17= 2R 0 so 34= 2 x 17 + 0
So the GCF is 17.
To find the lowest common multiple, multiply the two original numbers.
425 x 187 = 79, 475
Then divide that by the GCF that we just found.
79, 475 / 17 = 4,675
The lowest common multiple of 425 and 187 is 4,675.
I prefer prime factorization, because with this method you need to find or be given the GCF first. Finding the GCF is difficult because it can get confusing when dealing with remainders and lots of equations. Finding the lowest common multiple is a lot easier because you just have to divide two numbers but finding the GCF is more complicated than just using the prime factorizations method.





 Lesson 1 was review and a preview into the chapter. We reviewed what a variable and what an algebraic expression is. We also learned the difference between a monomial, binomial, trinomial, and a polynomial. (shown in image). With these polynomials, you can classify them by degree. “The degree of a monomial is the sum of the exponents of its variable(s)” and “the degree of a polynomial is the degree of the term with the highest degree.” After we learned how degrees work, we started to add and subtract polynomials. At first, with algebra tiles, then, just algebraically.
Lesson 1 was review and a preview into the chapter. We reviewed what a variable and what an algebraic expression is. We also learned the difference between a monomial, binomial, trinomial, and a polynomial. (shown in image). With these polynomials, you can classify them by degree. “The degree of a monomial is the sum of the exponents of its variable(s)” and “the degree of a polynomial is the degree of the term with the highest degree.” After we learned how degrees work, we started to add and subtract polynomials. At first, with algebra tiles, then, just algebraically.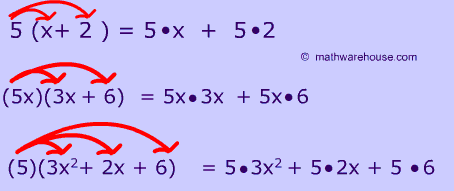 In lesson 3, We expanded on what we knew and learned how to multiply two binomials together. In this lesson, there were two models, algebra tiles and an area diagram, however I prefer to solve algebraically. Again, we expanded on the distributive property concept. The distributive property for two binomials is as follows: (a+b)(c+d) = a (c+d) b (c+d)= ac +ad +bc +bd.
In lesson 3, We expanded on what we knew and learned how to multiply two binomials together. In this lesson, there were two models, algebra tiles and an area diagram, however I prefer to solve algebraically. Again, we expanded on the distributive property concept. The distributive property for two binomials is as follows: (a+b)(c+d) = a (c+d) b (c+d)= ac +ad +bc +bd. angle in a right triangle. In order to do this, you need to know at least two side lengths of the triangle. And then you use a trig ratio (SOH CAH TOA) and plug in the numbers to solve. I also learned about the angle of elevation and the angle of depression. (Image shown). The angle of elevation is measured upwards from the horizontal line, while the angle of depression is measured downwards from the horizontal line. I learned how to apply this knowledge to solve word problems.
angle in a right triangle. In order to do this, you need to know at least two side lengths of the triangle. And then you use a trig ratio (SOH CAH TOA) and plug in the numbers to solve. I also learned about the angle of elevation and the angle of depression. (Image shown). The angle of elevation is measured upwards from the horizontal line, while the angle of depression is measured downwards from the horizontal line. I learned how to apply this knowledge to solve word problems.