This week in Pre-Calc 11, we continued on with our quadratic equations. We started inequality’s and how to solve them. We still use the factoring- 1-2-3 method, which is: one thing in common, difference of squares and then the longer way of doing the box or decomposition.
An inequality is a symbol that shows if the expression is greater then, greater than or equal to, less than and less than or equal to zero.
When doing an inequality you’re trying to show where the parabola is either greater than 0, or less then depending on what the inequality sign is. The x axes is split into three parts by the parabola. It is good to draw out something like this when you’re doing the inequality so you can see where it is above or below zero.

Now I am going to show you have to solve an inequality.
Step 1: When you first get your equation, get your zero pairs. Just like you would do to find the x-intercepts.

Step 2: Draw a X axes and put your numbers down. Next draw a parabola so you can see what is going to happen. In our example you can see it is asking where is it less that or equal to zero. So I know by just my drawing it is going to be in section three.

Step 3: Next write out your equation without putting int he symbols yet. You know that x is somewhere in between -7 and 2, that is why you write it out like that.

Step 4: Now we have to put in our symbol. And how you do that is you know for x to be in the middle section it must be greater than or equal to -7, because if it was less than it would be in section1, but it has to stay in section 2. And x must be less than or equal to 2. And same thing, if it was bigger than 2 it wouldn’t be in the middle section anymore.
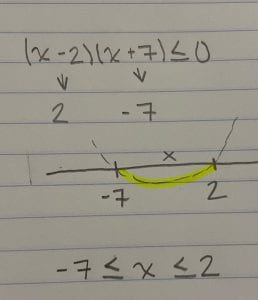
And I just wanted to show what it would be if the question was (x-2)(x+7)>0. This would be different because this is where the parabola is above zero. So section 1 and 3. And for it to stay in section 1 x has to be less than -7, and for 2 to stay in section 3, x has to be greater than 2.

In my opinion, drawing out the picture really helps. Without it I can’t really visualize what is happening but once you draw it out it becomes very clear, what is happening.