Month: November 2021

This week in Pre-Calc we started our rational expressions unit. Which involves a lot of factoring and “canceling out” like terms to get your expression down to its simplest form possible. One thing to remember is that something like “x+5” is like one number, so if we had x above that, the two x’s could not cancel out.

Example question

Step 1: The first thing I am going to do is simplify the denominator. You don’t need to do it in any particular order but I find it easiest to do it this way. I notice that 81 is a perfect square same with x^2  and it’s a subtraction, so I know this is a difference of squares. Meaning that I take the square root of 81 (9), and do (x+9)(x-9), and when foiled back out will equal to x^2-81.

Step 2: Now I am going to deal with the denominator. When I look at the pattern of the equation I am going to see this is a product and sum question. What multiplies to -18 and adds to 7? -2,9. If you check -2×9=-18 and 9+-2=7, so this is going to work. Now because there is no number in front of x^2 I can just put them in the brackets.

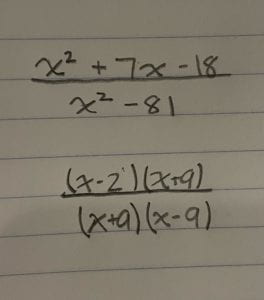
Step 3: Now I am going to cancel out like terms and “clean up” my rational expression. I can see (x+9) on the top and bottom, meaning they cancel out to an invisible 1.

Step 4: Now the last thing I need to add into my answer is the non-permissible values. Meaning numbers that if put in the place of x in the denominator would equal to 0, which we can’t have. Go through your entire equal and do the non permissible values for the whole entire equal, every line of work. Sometimes the numbers can change or cancel out. So here, I can see the x cannot equal +9, and if I go up to my second line of work I can see if I insert -9 into the equal it would equal 0. so that will be my second non-permissible value.

And that is it for simplifying down rational expressions! Something to note** (x-1)(1-x) aren’t the same!!

This week in Pre-Calc 11, we continued on with our quadratic equations. We started inequality’s and how to solve them. We still use the factoring- 1-2-3 method, which is: one thing in common, difference of squares and then the longer way of doing the box or decomposition.

An inequality is a symbol that shows if the expression is greater then, greater than or equal to, less than and less than or equal to zero.

When doing an inequality you’re trying to show where the parabola is either greater than 0, or less then depending on what the inequality sign is. The x axes is split into three parts by the parabola. It is good to draw out something like this when you’re doing the inequality so you can see where it is above or below zero.

Now I am going to show you have to solve an inequality.

Step 1: When you first get your equation, get your zero pairs. Just like you would do to find the x-intercepts.

Step 2: Draw a X axes and put your numbers down. Next draw a parabola so you can see what is going to happen. In our example you can see it is asking where is it less that or equal to zero. So I know by just my drawing it is going to be in section three.

Step 3: Next write out your equation without putting int he symbols yet. You know that x is somewhere in between -7 and 2, that is why you write it out like that.

Step 4: Now we have to put in our symbol. And how you do that is you know for x to be in the middle section it must be greater than or equal to -7, because if it was less than it would be in section1, but it has to stay in section 2. And x must be less than or equal to 2. And same thing, if it was bigger than 2 it wouldn’t be in the middle section anymore.

And I just wanted to show what it would be if the question was (x-2)(x+7)>0. This would be different because this is where the parabola is above zero. So section 1 and 3. And for it to stay in section 1 x has to be less than -7, and for 2 to stay in section 3, x has to be greater than 2.

In my opinion, drawing out the picture really helps. Without it I can’t really visualize what is happening but once you draw it out it becomes very clear, what is happening.

This week in Pre-Calc we finished up our quadratic functions unit. In this blog post I am going to show how you can look at a graph and figure out the equation. For this blog post I am going to focus on how to put it into the vertex form of the equation.

For this blog post I am going to use this graph as example:

Step 1: So to start off with I am going to look at the vertex.  I know that my x value of the coordinate (5) is going to be inserted into the equation, In the position (x-5). But we need to flip the sign to negative. If we started with a negative it would flip to positive.

Step 2: Now I can take my 2, from the y part of the coordinate and add +2 after my bracket, to show it is going to have a vertical translation of +2 when you graph it.

Step 3: We have inserted all of the information we can from our vertex, we are going to need to use the given point to find our stretch. To do this we have to insert the x and the y values from our coordinate into the equation where there is an x or a y. So in this case our coordinate is (3,-2). so the -2 is going to replace y=, and the 3 is going to replace the x in the bracket.  But if you go back and look at the original graph, it was congruent to the parent function, meaning there isn’t a stretch.

Step 4: The final thing we have to do is notice the parabola is a maximum so there has to be a negative out front of the bracket.

 

I’ll do an example on how to find the stretch. Let’s say we found the first part of our equation and the points given to us are, (-1,-13).

 

Step 1:  The first step is to insert our x and y values, like I explained above. Put the -1 in where the x is, and -13 where y is. I am going to put a in front of our bracket to represent the stretch.

Step 2: Now we have to solve this equation. I am going to start with inside the bracket and clean that up.

Step 3: Now I am going to square the 2. And add 5 to both sides to get rid of the -5, as it can’t be added to the 4a.

Step 4: My final step is to divide -8, by 4 because I have isolated the variable. When I do this I can see my parabola has a stretch of -2.

And that is what you need to know on how to look at a graph and put it into vertex form.

This week in Pre-Calc 11 we finished up our quadratic unit, reviewed for our midterm and started our analyzing quadratic equations unit. Although we haven’t gotten to in depth about this unit yet I am going to focus on the few things we have learned. In this blog post, I am going to show how to analyze a quadratic equation and what the equation can show us without even doing any solving or anything.

First of all, what is a quadratic equation? Compared to a linear equation? A quadratic equation is an equation with a degree of 2, while a linear equation has a degree of 1.

Let’s take this quadratic equation. There are certain things you can already know about this equation without using a graphing calculator or any other thing like that.

Y-intercept: The Y-intercept is where the line (s) touch the y axes. Without doing any graphing I can see that the Y-intercept in this equation is going to be 5. The Y-intercept is always the number in the equation without a variable.

X-Intercept: The X-intercept is where the line crosses the X axes. In this case when we graph it we see there is no X-intercept because the parabola never crosses the X axes.

The coordinates of the vertex:  The vertex is the bottom or top part of the parabola. So you can see in this case the coordinates are (2,3) because that is the lowest part of the parabola.

The equation of the axis of symmetry: The axes of symmetry is an invincible lines going right through the middle of the parabola. If you look at the graph you can see, if a line went right through the middle of it down to the X-axes it is going to be x=2.

The domain of the function: As you can see the domain is the restrictions on the X axis. But if you can see X can be anything. The parabola can go on forever. Therefor, XER, because x can be any value and be true.

The range of the function:  The range is the restrictions on the Y. As you can see the Y doesn’t go and can’t go lower than 3. So X≥3, because it can’t go down any lower than 3.

Those are a few simple things you can know about your quadratic equation before solving or doing any real work. One thing i’ll add is the x^2 value is + the parabola will be minimum, but if the value is – the parabola will be maximum, meaning it will open-down.