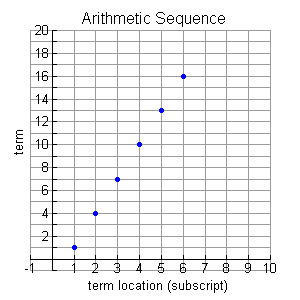
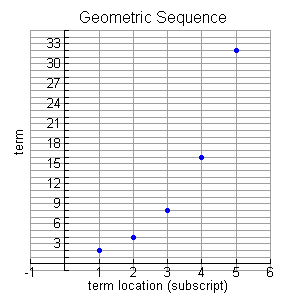
This week in Precalc I learned the acronym to help you when determining how to handle quadratic equations and trinomials: CDPEU (Can Divers Pee Easily Underwater). This acronym means Common Factors, Difference of Squares, Patterns, Easy, Ugly.

To start, you try and look for any common factors, which is pretty self-explanatory. If there are common factors, you’ll be able to reduce it right there before factoring.

Then, you see if there is a difference of squares, which also quite clear in what you need to do. If there is a difference of squares, you can factor it like so: a² – b² = (a + b)(a – b).

Next is patterns, which is telling you to look for a basic pattern such as a trinomial layout like: a number.

After that, see if it’s an easy question, where you can factor it easily with two numbers that multiply to the end term and add to the middle term.

Finally, check if it’s an “ugly” expression, meaning you’ll need to do some more work to solve that specific question, such as grouping or guess and check.

All in all, that’s the best way to identify and figure out how to solve various equations and expressions.

This week in math I learned about infinite geometric sequences, series, and their respective formulas and graphing. There are two different kinds of infinite geometric sequences and series: converging and diverging.

For a diverging geometric series, the sum is infinite, and thus the graph will constantly grow. No matter the numbers, any diverging series has a ratio greater than 1 or less than -1, and will always have no sum. Graphs for diverging series’ look like this:

For a converging geometric series, the sum is . The ratio must always be less than 1 and greater than -1, and because of this, the graph will always get smaller, with the sum being finite. This is a graph for a converging series:

This week in math, I learned of the usefulness of graphs for checking arithmetic or geometric sequences. You can easily identify if a sequence is geometric, arithmetic, or neither with a simple graph.

An arithmetic sequence will always be a simple linear graph, meaning it will appear as a straight line.

A geometric sequence will always consist of a curved graph, with the distance between each term on the graph increasing each time. This is a bit harder to identify, but can still be helpful.

So, I learned if you are ever positively unsure about a sequence, put it into a graph, and can get easy results.