Category: Grade 11

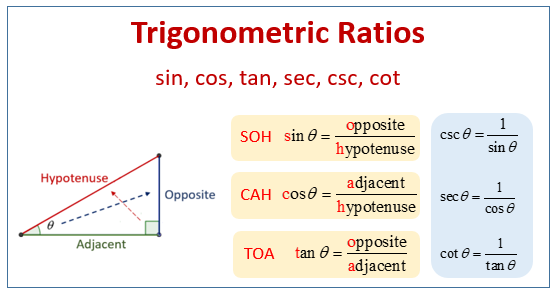
This week in Pre Calc 11 we continued our learning of trigonometry and were talking about rotational angles and their significance when plotting a triangle on the cartesian plane, one of the key takeaways from this week was that calculators are dumb and you need to remember that sometimes it will give you a reference and sometimes it will give the rotational angle depending on which ratio is used and if the ratio is positive or negative

for example a question said cos Θ = – and i went through and did the equation to solve for Θ and came up with () (-) and when i plugged it into my calculator i got an angle of about 84 degrees so i put it in quadrant one and called it a day, what i didnt think about at the time was that the original equation had stated that cos was negative meaning that the angle can only be in quadrant 2 or 3 making 84 a reference angle and the actual angles being 96 or 264

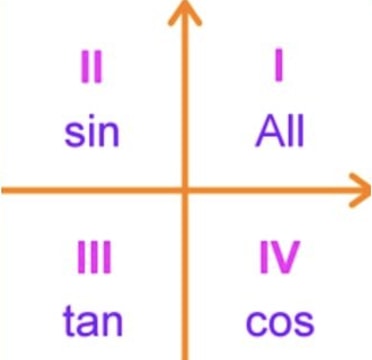
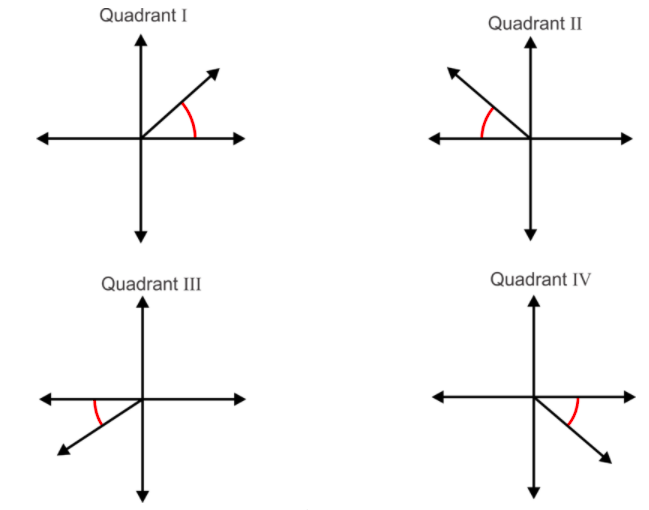
it is important to know how to tell if an angle is a rotation angle or a reference angle with a unit as calculator heavy as trig because the calculator will just give you a reference angle usually and you will need to determine which quadrants the angle resides in and then determine the angles

This week in pre calc 11 we were learning about trigonometry and the 3 ratios for right angle triangles (sine, cosine, and tangent) and their associated acronyms relating to their respective equations SOH CAH TOA for sin Θ = cos Θ and tan Θ and how to use those to solve for missing sides of a triangle.

For example i was given the adjacent side and the opposite side and needed to find the angle facing the opposite side and decided to use tan ratio, the mistake i made by doing so was using the tan ratio but instead of  i put it in as which gave me a completely different answer and one that involved me accidentally making up a fourth trig ratio

it is important to know for certain what your trig ratios are because they are the basic building blocks of everything to do with trigonometry and if you get those wrong you will be hopelessly lost in trig

This week in pre calc 11 we learned about radical expressions and equations and finding non permissible values in radicals and learning how to tell if the equation has no solution which comes in handy when solving and also helps confirm that you didn’t get a wrong answer you just got an answer that leaves the radical an imaginary number but you need to catch it, which leads me to my mistake.

during a test there was a section where we had to take a quadratic equation and state the npvs and find the answer and for both i got 5 but what i didnt catch because maybe i was stressed out by the environment of a test is that the numbers being the same meant that there were no solutions and i lost some marks because i didnt catch that the answer was imaginary

it is very important to know how to identify imaginary solutions because if you dont you may think that your algebra was wrong or maybe not think anything of the npvs and the answer being the same. if you arent able to identify if the answer is allowed or not you may think you did something wrong

This week in pre calc 11 we learned about radical expressions and equations and operations with said equations, learning things such as how to add subtract, multiply, divide, and simplify radicals.

For example a mistake I made was when i was adding two radicals together that had simplified to + and i thought you could cancel out the (x-5) (x-6) and (x-3) and add the remainder but you actually cant add fractions if they dont have common denominators and cant cancel out random radicals if they arent part of the same fraction

this is an important distinguishment to make because multiplying radicals vs adding radicals are two very different things and you cant use the same rules for both

This week in Pre Calc 11 we were learning about quadratic functions and equations and how to interpret things like the various equation forms that you can use to describe a function we also learned how to use these equations to find the 7 aspects of a parabola (vertex, line of symmetry, x intercepts, y intercepts, stretch, domain, and range) and while doing a question relating to making equations i noticed a mistake i made.

the question was asking me to write an equation based of the parent function of y=. the question had asked me to modify the equation to include a translation of 3 units left 8 units up and so I wrote +8 because i thought that since the modifier to x was negative and therefore the vertex would be in quadrant 3 at (-3,8) but actually in order to get the vertex to be at (-3,8) the equation would need to be +8 because in order for the x to go left it needs to be a positive number and the opposite for going right

here is a picture explaining it:

it is important to know how to do this as the vertex is the most important point on a parabola and plotting it incorrectly could potentially give you a parabola nowhere near the original

This week in Pre-Calculus 11, we were learning how to factor quadratics, and I made a mistake while trying to factor one of the expressions. I got focused on the middle term and thought that to factor the expression, I just needed to find two numbers that added up to that middle number. For example, I might have thought + 5x+6 could simplify to (x+4)(x+1) because $4+1=5$. However, I did not check if the product of 4 and 1 was correct, and it was not. The product of 4 and 1 is 4, not the constant term 6, so my factorization was wrong.

This mistake made me realize that factoring quadratics is not just about making the sum match the middle term. Both the sum and the product need to be correct. This mistake helped me understand that it is important to check both parts before finalizing my factorization. I also learned through this that I need to find the factors of 6 and make sure the factors I chose multiply to 6 while adding to 5 (in the case of this example, the correct factors would be 3 and 2, and the proper way to factor this expression would be (x+3)(x+2).