Tag Archives: Burtonmath10

Grade 10, Math 10

Math 10 Week 9

Leave a comment

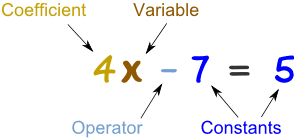
This week I learned how to find the GCF of a polynomial. This post will teach you how understand how to find the answer.  It seems very complicated at first but if you give it a chance you will learn very quickly. It is not as hard as it seems.

Ex. 9ab – 12ac

Step 1: Start with the numbers and find the greatest common factor. 

*The greatest common factor of 9 and 12 would be 3. 3 x 4 = 12 and 3 x 3 equals 9.

  1. Divide by the GCF and bring the 3 to the to the front of the brackets.

Step 2: Move to the variables. Start with the beginning of the alphabet

*Subtract the a with the lowest exponent from the rest of the a’s. Remember that a variable with no exponent has an invisible one.

* remember to bring the a with the lowest exponent out into the front of the brackets. If there is only one of the same variable then you just leave it because it is not common in both. It will be in the left overs.

Step 3: Repeat step 2 with the other variables if possible. 

See Pictures Below 🙂

 

Grade 10, Math 10

Math 10 Week 8

Leave a comment

This week we started polynomials. The first time you look at polynomials you will probably have a heart attack. But they’re not as hard as you think. In this post I will teach you what a polynomial is and some vocabulary as well as how to do a question.

Vocabulary:

Type– Types of polynomials

   Monomial- Consisting of one term.

 Binomial- An algebraic expression of the sum or the difference of two terms.

 Trinomial-  An algebraic expression of the sum or the difference of three terms.

 Polynomial- More than three parts/terms in the question.Constant

Degree– The highest exponent

Coefficient-The number in front of a variable.

Constant- In Algebra, a constant is a number on its own.

 

Ex. 3 – 2x + 7y + 4y – 2x + 8z – 9

Step one: highlight or underline like terms to start grouping. 

*like terms are numbers with the same ending.

3 – 2x + 7y + 4y – 2x + 8z – 9

Step two: Rearrange the numbers starting with the letter that comes first in the alphabet then go towards z. Do the constants last. Also go from greatest to least to stay organized.

– 2x – 2x  + 7y + 4y + 8z + 3 – 9

Step three: Combine like terms.

– 4x + 11y + 8z – 6

Type: This equation is a polynomial because it has more than three terms.

Coefficients: -4, 11, 8 *the coefficients poses the sign before it. (+/-)

Degree: If they don’t have an exponent the degree will be one. The only one without the exponent as 1 will be the constant. The constant will have an exponent of 0.

Constant: -6

 

Grade 10, Math 10

Math 10 Week 7

Leave a comment

This weeks goal is to teach you how to solve an angle and side lengths in the Trigonometry Unit.

Vocabulary:

SOH: S = \frac{O}{H} or Sine = \frac{Opposite}{Hypotenuse} 

CAH: C = \frac{A}{H} or Cosine = \frac{Adjacent}{Hypotenuse}

TOA: = \frac{O}{A} or Tangent = \frac{Opposite}{Adjacent}

 

i) Question One: What is the Angle of JEP to the nearest degree? (How to find an angle knowing two side lengths)

Step 1: Label the triangle 

*According to the reference angle

  1. Across from the reference angle is called the opposite side (O)
  2. Across from the 90^o angle is the hypotenuse (H)
  3. And the left over side is the adjacent side (A)

 

 

 

 

 

 

 

Step 2: Determine which ratio to use

Use the clues from the triangle. We will be using Cosine because we have the clues from the Adjacent and hypotenuse sides. (CAH)

 

 

 

 

 

 

 

 

 

 

 

 

Step 3: Write the equation

The cos angle is unknown so we will be writing it like :

 

Step 4: Get the variable by itself/Solve

*when moving the COS to the other side of the equation it becomes COS^-1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ii) Question two: What is the side length of AP to the nearest degree. (How to find the side length of a triangle knowing one side length and one angle.)

 

 

 

 

 

 

 

 

 

Step 1: Label the Triangle

*According to the reference angle

 

 

 

 

 

 

 

 

 

 

 

Step 2: Determine the ratio

Use the clues from the triangle. We will be using Tangent because we have the clues from the adjacent and opposite sides. (TOA)

 

Step 3: Write the equation/Solve

*We don’t want the variable on the bottom. Reciprocate the fraction and what you do to one side you do to the other.

 

 

 

 

 

X= 50cm  

 

 

 

 

iii) Question Three: What is the side length of AK to the nearest degree. (How to find the side length knowing one side length and one angle .)

Step 1: Label the Triangle

*According to the reference angle

 

 

 

 

 

 

 

Step 2: Determine the ratio

Use the clues from the triangle. We will be using Sine because we have the clues from the hypotenuse and opposite sides. (SOH)

 

 

 

 

 

 

 

Step 3: Write the equation/Solve

 

 

 

 

*We don’t want the variable on the bottom. Reciprocate the fraction and what you do to one side you do to the other.

 

X= 51 cm

 

Grade 10, Math 10

Math 10 Week 6

Leave a comment

This week I learned some pretty cool connections between different shapes. I thought that it was so cool that everyone else should know them. This may even help you in the future with volume.

*All of the shapes have to have to same height and radius/width for this to be accurate*

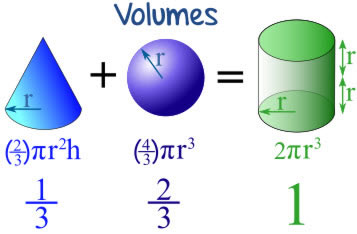Image result for connections between cones and cylandersOne cone with + One Sphere = The volume of a cylinder

 

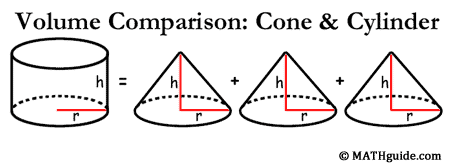Image result for connections between cones and cylanders Three cones = the volume of a cylinder

 

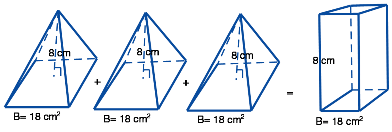Image result for Cylinder and Pyramid Three pyramids = A Square/rectangle

Grade 10, Math 10

Math 10 Week 5

Leave a comment

This week I learned how to convert from imperial to metric units that were cubed and squared. I was confused with this until it was explained to me in and the steps were all drawn out for me. So i decided to draw out all the steps for you 🙂

Ex. 2.5 m^2 = _______ ft^2

  1. Use the Conversion Factor to get to cm. * since you are going down the latter you will multiply to get to cm*
  2. When m^2 is on the top and the bottom it will cancel each other out.
  3. Place the exponent outside of the bracket and use the power law.
  4. After you use the Conversion Factor you will have it in cm.
  5. Now convert cm to inches. * We know that there is 2.54cm in 1 inch*
  6. After getting the measurement into inches, use the conversion Factor again to get to feet. * We know there is 12 inches in 1 foot*
  7. Then your measurement will be converted to ft^2

Answer: 2.5 cm^2 = 2.69 ft^2

See below for pictures!

Grade 10, Math 10

Math 10 Week 4

Leave a comment

Some Clarification

This week I cleared up a few misunderstandings.

  1.  I learned that exponents are very lazy and are only attached to whatever is in front of it. The only exception is when there are brackets. Then the exponent is forced to multiply its self with any hidden and visible exponents in the brackets.
  2. I also learned that if there are brackets and the exponent on the outside is negative it means the whole equation is unhappy, and you are allowed to reciprocate the entire thing. Then everything will become positive. But don’t forget to multiply the exponent on the outside to the ones on the inside.
  3. One other thing I learned is, if a negative number has a negative exponent it does not become the coefficient does not become positive when moved to become happy. You also need to remember that if the negative coefficient has brackets it will be a different answer than without. Make sure you watch for this common mistake 🙂

See below for pictures

Grade 10, Math 10, Tutorials

Math 10 Week 3

Leave a comment

This week we learned about exponents. I was was having trouble simplifying equations with negative exponents. We ended up going over negative exponents and how to deal with them. You need to make sure you leave all the exponential answers in positive form and to do so you need to…

Vocab: Multiplication Law – Add the exponents when they have the same base. Ex. 5^6\cdot5^2 = 5^8

Division Law – Subtract the exponents when they have the same base. Ex. \frac{5^6}{5^2} = 5^4

Integral (Negative) Exponent Law – Place the coefficient with the negative exponent on the other side of the division line to make the exponent become positive.

Work

  1. Find all the hidden exponents.
  2. Place all the coefficients with negative exponents on the other side of the divide line and then the exponents will become positive.
  3. Use the multiplication Law
  4. Use the Division Law
  5. Come the two parts
  6. If needed use another Exponent Law.

You have the answer

See Below for Pictures 🙂

Grade 10, Math 10, Tutorials

Math 10 Week 2

Leave a comment

This week I struggled with being positive. I wasn’t quite understanding how to convert mixed radicals to simplest form when it has an exponent of 3 or 4. I was getting very frustrated and thought I was going to fail the numbers test. I ended up going in after school and received help from a friend. I now understand it and i’m able to explain it to others.

Ex. 3\sqrt[3]{162}

Vocab:

Radical – The radical is the number under the line Ex. \sqrt{162}

Coefficient – The Coefficient is the Larger number on the outside Ex.  3\sqrt{162} 

Index – The index is the little number on the outside. Ex. 3\sqrt[4]{162}

 

How to convert the mixed radical into simplest form you need to:

  1. Find all the prime factors from the radical, using a factor tree or a factor table.
  2. Bring the coefficient over to the radical side. *** Any time that you are bringing in something from the outside in, the index should always come with it. There will be two now. One on the outside and one on the inside. (When it is attached to a number it is called an exponent).
  3.  Break down the 3^4 into its full form.
  4. Circle any groups of 4 that you see.
  5. One Group of four  = One of that number. Two groups = Two of the number.
  6. Bring the two 3s outside.
  7. Multiply the 3s together
  8. You now have the simplest form of 3\sqrt[4]{162}

See below for pictures

Grade 10, Math 10, Tutorials

Math 10 Week 1

1 Comment

This week I learned how to find the Lowest Common Multiple of 2 or more numbers. This is something I struggled with earlier this week. While doing my homework, I compared my answers with the real ones and when I got something wrong I retraced my steps and fixed any errors.

To find the Lowest Common Multiple of: Ex. 12, 30, and 105

  1. Create a factor tree or factor table.
  2. Sort the prime numbers from lowest to highest for 12, 30 and 105
  3. make into exponents.
  4. sort into groups- Notice that there is sometimes a prime number that is not a prime factor of another number. In this case you need to make that prime number to the power of 0 in the group that does not have that prime factor. Ex. 2 is a prime factor of 12 and 30 but not of 105. you need to write it like this- 12= 2 to the power of 2, 30= 2 to the power of 1 and, 105= 2 to the power of 0.
  5. You have now sorted into groups 🙂
  6. Chose the highest exponent from each group.
  7. Multiply the numbers you have chosen
  8. You should be left with the LCM of 12, 30 and 105. Good Job!

See below for pictures