Pre Calculus 11 Week 11: Graphing Linear Inequalities in Two Variables

April 29, 2018 jessicap2015 Leave a comment

This week in week 11 we started Graphing Inequalities. The majority of this is related to our graphing from last year in grade 10 math.

Linear graphs are known as straight line graphs with the equation of y=mx +b.

m is the slope ( $\frac{rise}{run}$ ) b is the y intercept

For example: $y =\frac{1}{2}x + 6$ on a graph looks like:

Now when graphing inequalities you have to find a sign that will have a true statement after you have chosen a point on the graph to substitute x and y.

$\star$ Note that > and < are broken lines on the graph and $\underline{<}$ and $\underline{>}$ are solid lines like the above graph ( because it is equal to so it includes the line)

$0 < \frac{1}{2}x + 6$ (greater than zero)
$0 \underline{<} \frac{1}{2}x + 6$ (greater or equal to zero)
$0 > \frac {1}{2}x + 6$ (less than zero)
$0 \underline{>} \frac {1}{2}x + 6$ (less than or equal to zero)

Now to graph the inequality you have to choose a point on the graph that makes the expression true for example:

$y < \frac{1}{2}x + 6$

$\star$ to make things easy use (0,0) as the point

$y < \frac{1}{2}x + 6$
$0 < \frac{1}{2}(0) + 6$
$0 < 0 + 6$
0 < 6

This statement is true because 0 is smaller than 6. This means that the side that has the coordinate of (0,0) will be shaded in. This will also have a broken line because it is not equal to.

Now when we change the sign to greater to (>) it will flip because 0 would not be greater than 6

$y > \frac{1}{2}x + 6$
$0 > \frac{1}{2}(0) + 6$
$0 > 0 + 6$
0 > 6
FALSE STATEMENT

If the sign was $\underline {>}$ or $\underline {<}$ the line would be solid.

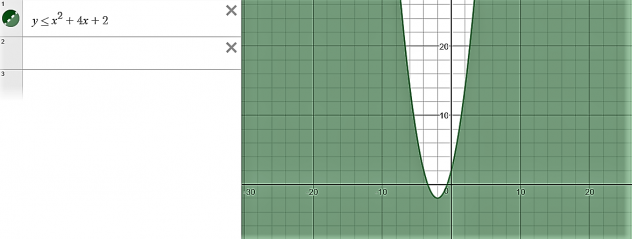
You can also graph a parabola

example: $y = x^2 + 4x + 2$

Step one: Graph the parabola by putting it into standard form.

$y = x^2 + 4x + 2$
$y =\underbrace{x^2 + 4x + 4} - 4 + 2$
$y = (x + 2)^2 -4 + 2$
$y = (x + 2)^2 -2$

Graph it from here.

Step two: chose a point on the graph and make a true statement.

$y \underline{<} x^2+4x+2$
$0 \underline{<} 0 + 0 +2$
$0 \underline{<} 2$
TRUE STATEMENT, 0 is smaller than two

The side with (0,0) as a coordinate will be shaded in and the line will be solid because it is equal to.

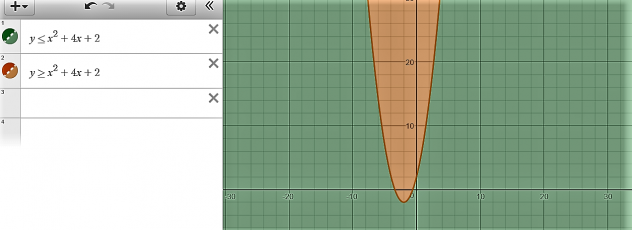
Now if the sign was change the inside of the parabola would be shaded in.

This is how to graph inequalities with linear equations as well as quadratic equations.

Grade 11, Math 11

Pre Calculus 11 Week 10: Reviewing Factoring with Substitution

April 29, 2018 jessicap2015 Leave a comment

Last week in Pre Calculus 11 we mostly reviewed for our midterm exam. As I was studying I came across a few things that I totally forgot about. Things that would help make my math life easier, like how to use substitution when factoring. This is helpful because it is simple, faster, and not as messy as factoring without this trick. I will quickly review how to do this.

Example: $3(2x-1)^2 + 14(2x-1) + 8$

Step 1: Substitute (2x-1) with a variable.

$\star$ Notice that there are two (2x-1), therefore you can use the same variable for both terms.

$3a^2 + 14a + 8$

Step 2: Factor $3a^2 + 14a + 8$

(3a + 2) (a + 4)

Step 3: Substitute (2x – 1) back into the factored form to replace the variable a.

(3a + 2) (a + 4)
(3(2x -1) + 2) ((2x-1)+ 4

Step 4: Distribute

(3(2x -1) + 2) ((2x-1)+ 4
(6x-3 +2)(2x-1+4)

Step 5: Simplify

(6x-3 +2)(2x-1+4)
(6x-1)(2x+3)

FINAL ANSWER

(6x-1)(2x+3)

To find the solutions make each factor equal to zero and solve for x:

6x-1=0 –> 6x=1 –> $x=\frac{1}{6}$

2x + 3=0 –>2x=-3 –> $x =- \frac{3}{2}$

This is how to use substitution while factoring. This is a very helpful and quick way to factor difficult looking equations.

Grade 11, Math 11, Uncategorized

Week 9: How to convert from General form to Standard form

April 16, 2018 jessicap2015 Leave a comment

This week in Pre Calc 11 I learned how to convert general form into standard form. I will show you how it uses completing the square but it a little different from last unit of solving quadratic equations. In this unit it helps us graph what the function will look like (this should look like a parabola)

Converting from General Form to Standard form.

ex/ $2x^2 -11x +4$

Step 1: Place brackets around $2x^2-11x$ , then divide by 2 to get $x^2$ instead of $2x^2$

$(2x^2 -11x) +4$
$2(x^2 - \frac{11}{2}x ) +4$

Step 2/3: Divide $\frac{11}{2}x$ by 2 and square it; place it in two blank spaces beside $\frac{11}{2}x$ one being added and one being subtracted.

$2(x^2 - \frac{11}{2}x +{blank} - {blank}) +4$
$2(x^2 - \frac{11}{2}x +\frac{121}{16} - \frac{121}{16}) +4$

Step 4: Multiply the 2 you factored out in step 1 to $\frac{121}{16}$ to remove it from the brackets.

$2(x^2 - \frac{11}{2}x +\frac{121}{16}) +4 -\frac{242}{16}$

Step 5: Factor the inside of the brackets.

$\star$ Hint: What you squared in step 2/3 is you factor.

$2(x^2 - \frac{11}{2}x +\frac{121}{16}) +4 -2\frac{242}{16}$

$2(x - \frac{11}{4})^2 -\frac{242}{16} + 4$

Step 6: Simplify

$2(x - \frac{11}{4})^2 -\frac{242}{16} + 4$
$2(x - \frac{11}{4})^2 -\frac{121}{8} + 4$
$2(x - \frac{11}{4})^2 -\frac{121}{8} + \frac{32}{8}$
$2(x - \frac{11}{4})^2 -\frac{89}{8}$

Final Answer: $2(x - \frac{11}{4})^2 -\frac{89}{8}$

You can check if you have done your calculations correctly by using desmos.com

$\star$ notice how both equations line up perfectly, this means that both are equivalent.

Standard form can tell us:

Standard formula: $y= a(x-p)^2 +q$

a = 2

p = $\frac{11}{4}$

q= $-\frac{89}{8}$

Horizontal translation: $\frac{11}{4}$ units right

Vertical translation: $-\frac{89}{8}$

Vertex : ( $\frac{11}{4}$ , $-\frac{89}{8}$ )

Axis of symmetry: $\frac{11}{4}$

This is how you convert General form into standard form in the unit of Quadratic equations. The standard form can tell you a lot about what it looks like and how to graph it. This is my favorite form in this unit because it tells me so much information and it is very useful. 🙂

Grade 11, Socials 11

5 year Age Groups and Gender of Benin

April 11, 2018 jessicap2015 1 Comment

Find the dependency ratio, is it high or low?
- 83.5% dependent. It is high.
Describe the situation in the country based on the info in your population pyramid (births, deaths, health, age, male/female, type of pyramid, stage in DTM etc.)
- High births, which are going to be dependent on the working age cohort, we have more kids than adults. We have less deaths than births; meaning they are getting an enhanced health care system/ everything is evolving. There are slightly more women than men in this country. This is an expanding pyramid. This is around stage 2.
Explain what the country needs to prepare for in the near future and why you think that. (health, population, business, policies, etc. Connect this to your observations)
- This country needs to keep making medicine, needs to increase food production, needs to make more schools and hospitals. They might need to make a policy of how many kids you are allowed to have if the population continues to increase at the rate its going. The health of these people are generally good but they die off around 80, but since there are high birth rates the death rate will increase later on so the country might want to make room for cemeteries and they might want to start businesses that help elderly people, like transportation or have more senior homes.

Grade 11, Math 11

Week 8: General Form, Quadratics

April 9, 2018 jessicap2015 Leave a comment

This week I learned many cool and fascinating facts about the general form of a quadratic equation ( $ax^2 + bx +c$ ) as well as analyzing $y=a (x-p)^2 + q$

General form

$x^2$ :

Positive – Open upward
Negative – Opens downwards

bx:

is a mixture of both $ax^2$ and bx so it can differ

Is the y axis

Analyzing equation: $y=a (x-p)^2 + q$

using this formula can tell us a lot of things that will help us graph the equation. In fact it will tell us 8 helpful clues.

ex. $latex -2(x+2)^2 – 1

Vertex: the vertex will be p and q … (-2,-1) * p is always backwards from the formula because in the original equation it is (x – p) therefore it has to be a negative number for it to become positive in the new equation.
Axis of symmetry: This will be p because it is the x value on a graph …-2
Opens up or down: This is determined if $x^2$ is negative or positive. If it is negative it will be opening down, and if it is positive it will be opening upwards… Opens down because it is -2
If it is congruent to $y = x^2$ . This means that the pattern of the graph would be 1, 3, 5. Meaning 1 over 1 up, 1 over 3 up, 1 over 5 up etc. If it does not follow the 1,3,5 rule it means that a has a value different from -1 or 1. Say a = 4, multiply 4 to each number from the original pattern. ex/ 1,3,5 is now equal to 4, 12 , 20 etc. This pattern will also tell us if the parabola will be stretched or compressed. If 1> a < 0 ( fraction ) it means that the parabola will be compressed. If 1 < a > 1 it means that the parabola will be stretched…. this equation is congruent to y = $-2x^2$ , it is being stretched because 2 > 1, it is negative so it will be flipped upside down but the structure is the same. (congruent)
Minimum or maximum: If a is positive, it will have a minimum. If a is negative it will have a maximum… It has a maximum of -1
Domain. We know the XER because the parabola never ends.
Range: If a is positive y will be greater than the minimum. If a is negative, y will be smaller than the maximum… y < -1, yER

IMPORTANT

$latex y = 3x^2 (x – 3)^2 + 4

The horizontal translation will be 3 units to the right even though it says -3.

I also learned that general form can be turned into the analyzing equation of $y=a (x-p)^2 + q$ by completing the square.

Here is a video that helped me understand how to complete the square

Socials 11

Data Set of Canada and British Columbia

April 4, 2018 jessicap2015 1 Comment

Data Set for Canada

Data Set for British Columbia

Math 11

Week 7: The discriminant

April 3, 2018 jessicap2015 Leave a comment

The portion of the quadratic formula that is the discriminant

A few weeks ago, before spring break we learned about the discriminant. This is used in the unit of quadratics and it is a portion of the quadratic formula. The discriminant is able to tell us the amount of solutions it will have.

# of solutions:

positive number : 2 solutions
negative number: no solution
equal to zero : 1 solution

. ex. $5x^2 - 9x + 4 = 0$

determine a, b, and c from the equation: a = 5 b= -9 c = 4
enter into the discriminant formula:

$b^2 - 4ac$
$-9^2 - 4(5)(4)$
$81 - 4(20)$
$81 - 80$ = 1

This number is positive, therefore, it has two solutions

Crosses the x-axis in two spots; 2 solutions

ex2/ $latex x^2 + 8x + 16 = 0

a = 1, b = 8, c = +16
$b^2 - 4ac$
$8^2 - 4(1)(16)$
$64 - 4(16)$
$64 - 64)$ = 0
(equal to zero) 1 solution
touches the x-axis in 1 spot: 1 solution

ex3/ $latex -2x^2 + 3x – 10 = 0

a= -2, b = 3, c= -10
$b^2 - 4ac$
$3^2 - 4(-2)(-10)$
$9 - 4(+20)$
$9 - 80$ = -71
(negative number) No solution

does not cross the x-axis, therefore it has no solution

This is how you would find the discriminant, as well as finding how many solutions it has. Using this can also help determine if the answer will be a rational or irrational number.

Jessica's Blog

Monthly Archives: April 2018