This week in pre-calculus we started our unit on trigonometry. We learned about Sine Law, it’s an equation on how to find the sides and the angles in a triangle all put into one instead of having to use separate equations to solve. If we’re solving for a side of the triangle we’ll use the ratio .

If we want to solve for the angle then we reciprocate the ratio and it’ll be .

To solve for side “a” then we’ll use the first equation.

ex/

once we rearrange and cross multiply we’ll get

This week we learned about rational equations which are different from the expressions we have been doing, because now we need to solve for the variable. Two ways to do this is by cross multiplying or by multiplying by the common denominator.

Here is an example of cross multiplying to solve for the variable:

This week in precalc we learned how to multiply and divide rational expressions. To do this the easiest way to start is to try and simplify it as much as possible before starting to multiply or divide, this will help to not have large numbers and have to simplify later on which can get complicated. Something to remember when dividing is to reciprocate the second fraction and we can now multiply it by the first fraction.

This week in PreCalc we learned about reciprocal functions and how to graph them in linear and quadratic functions. Reciprocal functions are very different graphs from absolute value functions and it’s important to notice the difference between them. When graphing reciprocal functions the two most important things are the asymptotes and the invariant points, these will help turn the parent function into the reciprocal function.

Ex/

Parent Function

Reciprocal Function

Absolute Value Function

This week we learned about absolute value functions. When you have an absolute value of a function, the line or parabola cannot enter the negative area of the y axis. It will reflect upwards when graphing.

ex/ y= -4x+5

the green is the original function and the purple is the absolute value of the function. You can tell from this graph that when the absolute values are placed it reflects back upwards.

This week in PreCalc we learned how to solve systems algebraically using substitution and elimination. Doing this will help us find the points of the intersection between the line and parabolas. Using substitution is when you have two separate equations and get one variable by itself so we can input it into both equations to find the intercept points.

Ex:

In Precalc this week we learned how to solve quadratic inequalities. When its greater than or equal to and less than or equal to, the line is solid. And when it’s just <,> the line is dashed. Then you have to shade one side of the line, to figure out which side to shade use a test point, you can generally use the point (0,0). If it’s true shade the side with that coordinate, if not shade the other side.

This week in pre-calculus we were reviewing for our midterm. There was a lot I had to re-learn this week but the one thing I struggled with the most was how to solve quadratic equations and putting it into the quadratic formula.

Example: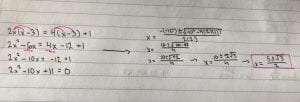

This week in pre-calculus we learned how to change an equation into general form to vertex form and vise versa. By changing it we get more information about the different key points on the graph which makes it easier to graph the equation.

To do this we need to complete the square.

Ex/ 

This week in precalc we learned about the key points in standard form/vertex form and how to use them to graph a quadratic equation.

the equation is

The coefficient a shows the stretch of the parabola if a = 1 its the  1-3-5 pattern, if a>1 the parabola gets skinner and if |a|<1 it gets wider. If a has a negative sign in front of it that means that it opens downwards.

The p is the horizontal translation, it shows if it moves to the right or the left of the graph. When it +p it’s moved to the left, but when it’s -p it’s moved to the right.

The q is the vertical translation, when its positive it’s moved upwards and when it’s negative it’s moved down the graph.

Also we can find the vertex it’s (p,q)