This week in Pre-Calc we learned about discriminants. A discriminant gives information about the roots of the quadratic equation. We use  to find the value.
to find the value.
- If it is less than 0, there are no real roots.
- If it is equal to 0, there’s one real root.
- If it is greater than, 0 there are two real roots.
Ex: 
a=2, b=-7 c=3
step 1: 
step 2: 
step 3: 
The discriminant is 25, because it is greater than 0, this means that this quadratic equation has two real roots.
This week in pre-calc we’ve been learning how to use factoring to solve quadratic equations. Something I challenged with at first was using the perfect square trinomial method because of all the steps involved.
Example: 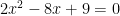
There are no two numbers that add to -8 and 9 so the first thing to do is move the 9 to the other side. Now we can find a something in common to take out of the 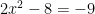
 before factoring the trinomial I factored out the 2.
before factoring the trinomial I factored out the 2. I moved the 9 back over and the +4 -4 are now there because we took the half of 4 which is two and the squared it to put it back in.
I moved the 9 back over and the +4 -4 are now there because we took the half of 4 which is two and the squared it to put it back in. the -8 is now there because the 2 in front of the brackets needs to be mulitiplied with the -4 in order to take it out of the brackets.
the -8 is now there because the 2 in front of the brackets needs to be mulitiplied with the -4 in order to take it out of the brackets. in this part the -8 is subtracted by the 9 and which gave us +1 and we moved it over to the right side of the equation.
in this part the -8 is subtracted by the 9 and which gave us +1 and we moved it over to the right side of the equation. =
=  divide both sides by 2 to get rid of the coefficient in front of the brackets.
divide both sides by 2 to get rid of the coefficient in front of the brackets. to get rid of the x-2 squared both sides need to be square rooted.
to get rid of the x-2 squared both sides need to be square rooted.- At this point we can see there’s a negative under the root which is not possible because we can’t square root a negative number. This means that this equation has no solution.
This week in precalc we learned about how to solve radical equations. Whenever we’re solving an equation we always have to do the same thing to both sides. After solving for the variable we always have to verify the solution to make sure it is a real root. when there’s a radical involved we have to square both sides to get rid of it, which is what I did in line to.
Example:
This week in precalc we learned about multiplying and dividing radicals. With multiplying radicals we use other techniques we learned like simplifying and foiling.
example: 
the first step is to foil :  +
+  +
+  +
+ 
after foiling the new expression will be: 
we can now simplifie the answer by finding perfect squares under the roots: 
after simplifying we get the final answer: 
This week we started our new unit on absolute values and radicals. It was a very short week and most of it was review from grade 10 math, except for the new term of what an absolute value is. Something I found hard to do at first was turning entire radicals into a mixed radical.
example 
first we need to find two numbers that multiply to 72, with one of them being a perfect square.


because 9 is a perfect square of 3 we can take that and put it as a coefficient leaving only the 8 under the root symbol.

this is our final answer.
This week in pre-calc 11 we learned about geometric sequences and series. An important part in these is the common ratio, it shows the difference between the terms by the term being multiplied by the constant.
The formula to find the CR is: 
Example: 4, 8, 16, 32
If you’re looking for the common ratio we need to divide 8 by 4.

You could also do  As long as you use a term that precedes
As long as you use a term that precedes 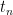 as the denominator you will get the right answer for the common ratio.
as the denominator you will get the right answer for the common ratio.
In the first week of Pre-Calc we learned how to find the sum of an arithmetic series. An arithmetic series is the sum of all the terms in an arithmetic sequence added together. We used the formula 
 to find the sum.
to find the sum.
In this formula N represents the amount of terms in the sequence. We replace  with the first term in the sequence and
with the first term in the sequence and  with the last term. Once you’ve filled in the variables in the fomula you divide n by 2. Then add the first and last terms together.
with the last term. Once you’ve filled in the variables in the fomula you divide n by 2. Then add the first and last terms together.
Ex. 2, 5, 8, 11, 14….59 

with this information we can solve for 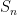




to find the value.
