Everything I know about exponents
 =
= 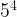
- A power means that you multiply that number (base) a certain amount of times (exponent). All in all, a shorter way of showing repeated multiplication.
 = (
= ( )
)  (
( )
)  (
( )=8;
)=8; 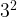 = (
= ( )
)  (
( )=9
)=9 =
= 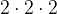 ;
; 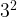 =
= 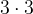
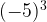 =
= 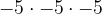 = -125
= -125- When expression is
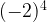 , that means
, that means  =16. When expression is
=16. When expression is 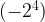 , that means
, that means 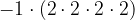 = -16. When expression is
= -16. When expression is  , it is same as second expression.
, it is same as second expression.
- When you are multiplying exponents with the same base, you add the exponents. Example:
 =
=  =
= 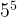 . When dividing exponents with the same base, you subtract the exponents. Example:
. When dividing exponents with the same base, you subtract the exponents. Example: 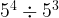 =
= 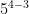 =
= 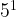 .
.
- When product/quotient is raised to exponent, you do the exponent first then evaluate the power. Ex:
 =
= 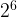
- When exponent is 0 and base is not 0, the answer is always 1. Ex:
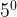 = 1.
= 1.
 =32,
=32, 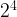 =16,
=16,  =8,
=8,  =4,
=4, 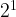 =2,
=2, 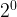 =1. As the exponent decreases by one, the answer divides by two. Therefore, it divides by the base, which shows why
=1. As the exponent decreases by one, the answer divides by two. Therefore, it divides by the base, which shows why 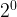 =1.
=1.- When you have negative exponents, you do the reciprocal of the base to make the exponent positive. Ex:
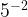 =
= 
 =4,
=4, 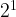 =2,
=2, 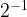 =
=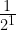 =
=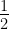 ,
, 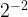 =
=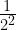 =
= . Therefore, when exponent number is same (2,-2), the answer for the positive exponent is always in the denominator for the negative exponent. Ex:
. Therefore, when exponent number is same (2,-2), the answer for the positive exponent is always in the denominator for the negative exponent. Ex:  =8;
=8; 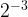 =
=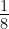 .
.- When base is integral:
 =-64. A trick for this is that if you have an odd number of exponent, the answer will always be negative. When the exponent is even, the answer will always be positive. Ex:
=-64. A trick for this is that if you have an odd number of exponent, the answer will always be negative. When the exponent is even, the answer will always be positive. Ex: 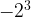 =
=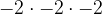 =-8.
=-8. 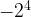 =
=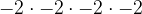 =16. When base is a variable, nothing changes to the base because we only make the assumption that the base is positive, so we just do the exponent laws. Ex:
=16. When base is a variable, nothing changes to the base because we only make the assumption that the base is positive, so we just do the exponent laws. Ex: 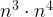 =
= =
=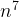 .
.
 =
=  . Error= product law applies so you add the exponents, not multiply. Correct=
. Error= product law applies so you add the exponents, not multiply. Correct= =
=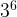 =729
=729- 3+
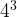 -11=3+
-11=3+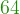 -11=
-11=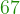 -11=56
-11=56
- With sums and differences, you use BEDMAS without any certain laws. Sum:
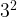 +
+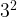 =9+9=18. Difference:
=9+9=18. Difference: 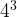 –
– =64-16=48.
=64-16=48.
- When
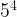
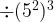
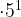 =
=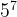 , this equation is incorrectly done. The power law comes into effect first, so you do
, this equation is incorrectly done. The power law comes into effect first, so you do 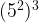 first, which is
first, which is 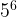 . Then you add the
. Then you add the 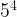 with the power law exponent, then subtract it with the
with the power law exponent, then subtract it with the 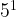 . When
. When 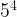
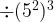
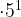 =
= , this equation is correctly done.
, this equation is correctly done.
- Question: John is trying to measure the side length of his house which is done as a shape of a cube. He figured out that the volume of his house is 8000
 . What is the side length of the house? Volume=8000
. What is the side length of the house? Volume=8000 . Side length=
. Side length=![\sqrt [3]{8000} \sqrt [3]{8000}](https://s0.wp.com/latex.php?latex=%5Csqrt+%5B3%5D%7B8000%7D&bg=ffffff&fg=000000&s=1) =20
=20
- Question: A flower has grown a squared amount of its normal height in a month. its normal height is 3 cm. What is its current height? Current height=
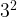 =9 cm
=9 cm
- When you have multiple exponent laws in an expression, normally you do the power law first, the zero law if any, then it varies, but normally the negative law, the product law, then the quotient law last. Ex:
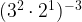
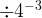 =
= 
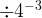 =
= 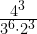 =
= 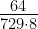 =
= 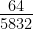 =
= 
=
= (
)
(
)
(
)=8;
= (
)
(
)=9
=
;
=
=
= -125
, that means
=16. When expression is
, that means
= -16. When expression is
, it is same as second expression.
=
=
. When dividing exponents with the same base, you subtract the exponents. Example:
=
=
.
=
= 1.
=32,
=16,
=8,
=4,
=2,
=1. As the exponent decreases by one, the answer divides by two. Therefore, it divides by the base, which shows why
=1.
=
=4,
=2,
=
=
,
=
=
. Therefore, when exponent number is same (2,-2), the answer for the positive exponent is always in the denominator for the negative exponent. Ex:
=8;
=
.
=-64. A trick for this is that if you have an odd number of exponent, the answer will always be negative. When the exponent is even, the answer will always be positive. Ex:
=
=-8.
=
=16. When base is a variable, nothing changes to the base because we only make the assumption that the base is positive, so we just do the exponent laws. Ex:
=
=
.
=
. Error= product law applies so you add the exponents, not multiply. Correct=
=
=729
-11=3+
-11=
-11=56
+
=9+9=18. Difference:
–
=64-16=48.
=
, this equation is incorrectly done. The power law comes into effect first, so you do
first, which is
. Then you add the
with the power law exponent, then subtract it with the
. When
=
, this equation is correctly done.
. What is the side length of the house? Volume=8000
. Side length=
=20
=9 cm
=
=
=
=
=
Exponents are not easy to understand. I think that he understands about these. He was doing good.
-Jason’s mom..
I think that you have a really good understanding of exponents. You explained everything in full sentences and good explanations.
-Jesse Rowley