Category Archives: Math 11
Week 14 in Pre Cal 11
Solving Equations
This week during pre calculus 11, we worked on solving equations including ones that were already simplified and ones that weren’t.
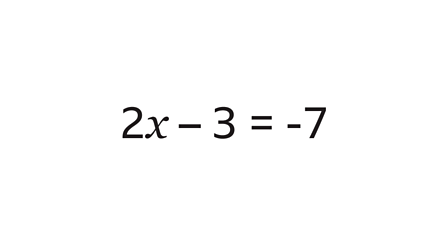
To start off explaining how to do this form of algebra, I’ll start by saying that if you have a subtraction or addition equation with an equal sign within it, you must end up adding or subtracting the part that requires that.
Like for example if the equation was ( +
= 3), you could immediately add the first (2) making it (
= 3)
But as we know, to add or subtract fractions, they must have the same denominators and sometimes (most often) the fractions won’t start off by having the same ones. So your first step in most equations will be to find the common denominator.
An example of this could be ( –
= 6) you could multiply the second fraction by (x) (numerator and denominator to make the fraction equivalent to its original form) which would then make the equation (
–
= 6) which you can then find the difference which ends up being, (
= 6).
Though I’m sure you may be thinking how this equation looks very complicated now! So the next step if we were to keep this same question would be to make it look a bit less complicated. You would do this by simply also giving the fraction after the equal sign the same common denominator as the one before the equal sign.
So in this case, we would take the (= ) and times the numerator and denominator by (3x) which would end up being (
=
) and since both sides of the equation now have a common denominator, you can completely take away all the denominators which makes it (-4x+1 = 18x). You can take away the denominators because now that you’ve multiplied the numerators to get that common denominator, the numerators are also equivalent to each other.
Now all you must do to the remaining numbers is add like terms! you can move the (-4x) to the (18x) side which then makes it (18x+4x = 1) which then adds to (22x = 1).
Now I made this question myself just to demonstrate so of course it’s not going to be a perfect whole number answer, but you would divide both sides of the equation by (22) to get the (x) on its own to figure out its value, so then end answer would be (x = ).
Another way to have found this answer would have been to instead of finding the common denominator for both sides of the equal sign, we could have cross multiplied!
Cross multiplying is where you multiply the numerator of the left side to the denominator of the right side, and the denominator of the left side to the numerator of the right side. Both of these answers would then go on opposite sides of the equal sign and replace the fractions you had.
So for example if we were to take ( =
) pur answer would be (8x = 15) which you’d then divide to get the (x) variable on its own, to make (x =
).
You have the ability to choose to use either of these types of ways to simplify and then solve the equations you’ve been given. I personally prefer the finding a common denominator most of the time, because sometimes the number are very large for cross multiplying which can make it take a lot longer than needed to solve the equation but it truly depends on the specific equation you are given.
Week 1-Math 11-Real Numbers
Though it’s not often thought of, there are many different types of numbers in our daily lives. Everything is considered a real number but it is then divided into 2 categories, the rational numbers and the irrational numbers. For example, the sqaure root of 25 is 5 which is rational because it can be put into a fraction (5/1) While the square root of 5 is has an irrational number as it’s answer because the answer has decimals wihtout any pattern and can not be put into a fraction.

Within the rational numbers, there are integers which are positive and negative numbers without decimals. Whole numbers, which are whole numbers including the number 0, and finally there are natrual numbers which are the numbers we were first taught as children (1,2,3,4… without including 0).

Irrational numbers MUST be non terminating (decimals do not ever end) and they also must be non repeating, meaning there is no pattern within the decimals. A great example of an irrational number is pie! (3.14…)
The reason I chose to do this post on the different types of numbers is because last year, though I remebered some of them, most would slip my mind and I belive they could definitely help me this semester and also help me understand more fully why certain problems are solved in a certain way!
