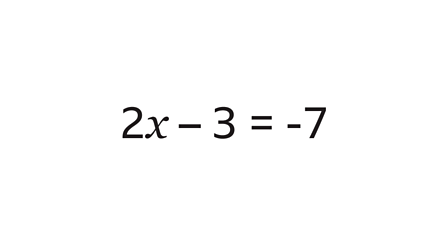Author Archives: Emma

Goal Setting Mid-Term

Posted on by
Reply

I can identify bias and contradictions in texts and writing, I can write a meaningful text for a variety of purposes and audience, and another strength of mine is I can express my ideas with evidence. My best example of this would be my Feminist Lens write where I identified small biases within the novel and wrote about how and why those may have happened and how to move forward as a society which I feel I went into great depth about and had a lot of fun writing.

I could improve my writing by learning more thoroughly how to insert quotes though it still confuses me which can make me forget to do them and then have to turn in my work late to complete such a small part. My goal is to hand assignments in on time since sometimes I simply forget about things and then lose the motivation to finish them when it’s already late. From now on I will work harder on asking questions when I don’t fully understand something so I can complete the assignments earlier.

The artifact I chose was Creative Thinking because I can, explain/recount and reflect on experiences and accomplishments not just of my own but also of others and I’m also able to write about it to explain those thoughts to those around me, which in my opinion, is an incredible thing to be able to do.

essay anxious people (1)

Week 16 in Pre Calc 11

Posted on by
Reply

This week, we started a new chapter which is Trigonometry! Last year in grade 10 during Trig, I did really well during the unit and for the unit test but when it came to the mid term, when trigonometry appeared, I had somehow completely forgotten the entire unit and how to do it all so I did pretty horrible on that part of the mid term, so this year when trigonometry was brought back, I was definitely a bit scared for if i would be successful and that definitely didnt help me to learn it.

But now that we’ve spent more time on it, i definitely feel more comfortable but I’m still not 100% there so i will most certainly be discussing it all with my tutor this weekend. It was also very interesting to learn how all of those triangles we’ve been working on since trig started have actually been on a graph this whole time and that makes so much more sense to me and has helped me fully understand the concept as a whole better aswell.

After my tutoring session, i’ve understood a lot more from this past week of mathematics. I had completely forgot how to truly find the angle or the length of a side by using the (Sin O = -3/7) type of equation, and the way you would do this is by moving the (Sin) over to the other side of the equal sign which turns it into (O = Sin^-1 (-3/7) which will equal to the degree you are looking for. I know that is last year’s work, but i had forgotten how to do it and you simply cannot build off last year without this peice of it.

Week 14 in Pre Cal 11

Posted on by
Reply

Solving Equations

This week during pre calculus 11, we worked on solving equations including ones that were already simplified and ones that weren’t.
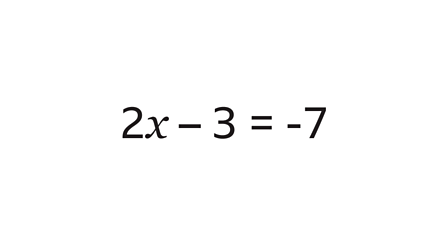
Solving equations with 𝒙 on one side - KS3 Maths - BBC Bitesize
To start off explaining how to do this form of algebra, I’ll start by saying that if you have a subtraction or addition equation with an equal sign within it, you must end up adding or subtracting the part that requires that.
Like for example if the equation was (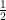\frac{x}{2} + \frac{1}{2}= 3), you could immediately add the first (2) making it (\frac{x}{2} = 3)

But as we know, to add or subtract fractions, they must have the same denominators and sometimes (most often) the fractions won’t start off by having the same ones. So your first step in most equations will be to find the common denominator.
An example of this could be (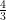\frac{1}{3x} – \frac{4}{3} = 6) you could multiply the second fraction by (x) (numerator and denominator to make the fraction equivalent to its original form) which would then make the equation (\frac{1}{3x} – \frac{4x}{3x} = 6) which you can then find the difference which ends up being, (\frac{-4x+1}{3x} = 6).

Though I’m sure you may be thinking how this equation looks very complicated now! So the next step if we were to keep this same question would be to make it look a bit less complicated. You would do this by simply also giving the fraction after the equal sign the same common denominator as the one before the equal sign.

So in this case, we would take the (= \frac{6}{1}) and times the numerator and denominator by (3x) which would end up being (\frac{-4x+1}{3x} = \frac{18x}{3x}) and since both sides of the equation now have a common denominator, you can completely take away all the denominators which makes it (-4x+1 = 18x). You can take away the denominators because now that you’ve multiplied the numerators to get that common denominator, the numerators are also equivalent to each other.

Now all you must do to the remaining numbers is add like terms! you can move the (-4x) to the (18x) side which then makes it (18x+4x = 1) which then adds to (22x = 1).

Now I made this question myself just to demonstrate so of course it’s not going to be a perfect whole number answer, but you would divide both sides of the equation by (22) to get the (x) on its own to figure out its value, so then end answer would be (x = \frac{1}{22}).

Another way to have found this answer would have been to instead of finding the common denominator for both sides of the equal sign, we could have cross multiplied!

Cross multiplying is where you multiply the numerator of the left side to the denominator of the right side, and the denominator of the left side to the numerator of the right side. Both of these answers would then go on opposite sides of the equal sign and replace the fractions you had.

So for example if we were to take (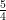\frac{2x}{3} = \frac{5}{4}) pur answer would be (8x = 15) which you’d then divide to get the (x) variable on its own, to make (x = \frac{15}{8}).

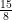You have the ability to choose to use either of these types of ways to simplify and then solve the equations you’ve been given. I personally prefer the finding a common denominator most of the time, because sometimes the number are very large for cross multiplying which can make it take a lot longer than needed to solve the equation but it truly depends on the specific equation you are given.

Week 1-Math 11-Real Numbers

Posted on by
Reply

 

Though it’s not often thought of, there are many different types of numbers in our daily lives. Everything is considered a real number but it is then divided into 2 categories, the rational numbers and the irrational numbers. For example, the sqaure root of 25 is 5 which is rational because it can be put into a fraction (5/1) While the square root of 5 is has an irrational number as it’s answer because the answer has decimals wihtout any pattern and can not be put into a fraction.

 

Within the rational numbers, there are integers which are positive and negative numbers without decimals. Whole numbers, which are whole numbers including the number 0, and finally there are natrual numbers which are the numbers we were first taught as children (1,2,3,4… without including 0).

Irrational numbers MUST be non terminating (decimals do not ever end) and they also must be non repeating, meaning there is no pattern within the decimals. A great example of an irrational number is pie! (3.14…)

The reason I chose to do this post on the different types of numbers is because last year, though I remebered some of them, most would slip my mind and I belive they could definitely help me this semester and also help me understand more fully why certain problems are solved in a certain way!