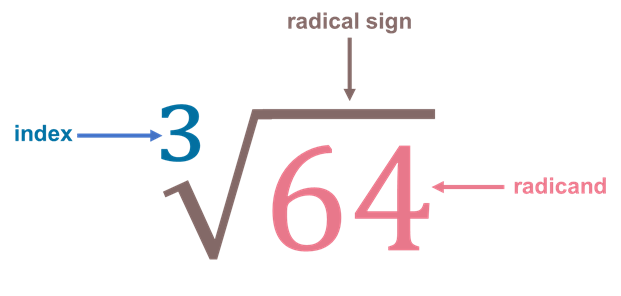Category Archives: Grade 11

Week 3 – PC11 – Exponents and Radicals

Posted on by

Question 1 #3 – PC 11 Skill Check 2

This week biggest mistake comes from the 2nd skills check where my answer could have been written in a better way. I chose this mistake as it’s important to understand how to deal with fractions when they come up in questions as it is typically daunting.

 

To correctly evaluate this question, you place the decimal over its correct place value. In this case, -2.5, the 5 is in the tens spot, thus we move the decimal over and change the fraction to: 

\frac{-25}{10}

 

Now, considering the exponent, the denominator becomes the index *flower power* and since exponents are considered lazy, the exponent only applies to the fraction and does not include the negative. We now have our answer of:

 – \sqrt[4]{\frac{25}{10}} -> simplified to:  – \sqrt[4]{\frac{5}{2}}

 

Week 2 – PC 11 – Exponents and Radicals

Posted on by

Question 3 #2 – PC 11 Chapter 1 Skill Check

This weeks mistake is from the first skill check. In evaluating \sqrt{\frac{150}{54}} , instead of first reducing the fraction I wrote both the numerator and denominator the product of two square roots and further simplifying. I chose this mistake as its common to overlook the simplifying of a fraction when dealing with other components such as a square root.

The first step in solving this question is to reduce \sqrt{\frac{150}{54}}  to its simplest form. This is done by dividing both the top and bottom numbers by 2 as its easiest to evaluate.

\sqrt{\frac{150}{54}} = \frac{\sqrt{75}}{\sqrt{27}}

Then, you can simplify further by dividing both the numerator and denominator by 3.

\sqrt{\frac{75}{27}} = \sqrt{\frac{25}{9}}

Now you can evaluate both the numerator and denominator as square roots.

\sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}} = \frac{5}{3}

This gives us the correct and final answer of: \frac{5}{3} 

 

Week 1 – PC 11 – Exponents and Radicals

Posted on by

 

Pg 12, Q3. f

 

 

 

 

I chose this mistake of the week from the Exponents and Radicals Lesson #2 assignment where I had overlooked the result.

  • To solve this question, we must evaluate both the numerator (top) and denominator (bottom) of the fraction using the fourth root.

4 in the index position, the small number next to the radical sign tells us that we need to find 2 numbers that when multiplied by themselves 4 times, produces our 2 values of our radicand, 1 and 256

\sqrt[4]{1} = 1 *(and -1 respectively) because 1 x 1 x 1 x 1 = 1  and \sqrt[4]{256} = 4 as 4 x 4 x 4 x4 = 265.

 

  • Where I went wrong in my initial attempt of this question is I evaluated the radicand to be equal to 4.

 

Our new fraction becomes \frac{1}{4} multiplied by the coefficient of -8. \frac{1}{4} (-8)

The last step is to multiply and simplify, luckily the multiplication of a fraction is fairly straight forward we work across to \frac{1(-8)}{4(1)}  = \frac{-8}{4} which can be simplified by 4 which gives us the answer -2

https://helpingwithmath.com/addition-subtraction-of-radical-expressions/