TOP 5 Math 10 things for the last math 10 blog post
Daniel's Blog
I'm You not me
Category: Grade 10 (page 1 of 3)
Systems of Linear Equations
word problems
We learned that in word problems we must identify the x and y; which in this case is the Balanced Fund & Emerging Markets.
The 1nd Equation: After identifying the x & y we create our equation: x+y=42000 since the sentence describes it as “invested into two different mutual funds,” as there is 2 different funds containing the the 3/4 x 56000$ it becomes x+y=42000
The 2nd Equation: 0.06x-0.03y=1590 is because x is a gain so it’s positive, the other is a loss but in the end it was a profit.
After completing the equations and solving it, we return to the original to fill in the x and y’s to see if it works. If it ends up the same as the answer then it’s correct.

This time we went over perpendicular lines and parallel lines and how they work.
Perpendicular lines can be represented by a 90* angle. It’s also when one fraction is a reciprocal of the other. like 3/4 becomes -4/3
Parallel lines can be described by two equal slopes like. 3/4 and 6/8
this time is how we calculated the Distance over something. If we want the slope of A and B
we take the coordinates (0,3) (4,6) and we use the equation m=y2-y1/x2-x1 or m=y1-y2/x1-x2 so get the slope=3/4
Then take the equation y=mx+b and put the slope in the equation: y=3/4x+b.
After successfully completing these steps you choose one of the two coordinates and replace the y and x with them.
6=3/4×4+b
which gives us the y-intercept/b
3=b
and there we have everything.
Systems of Linear Equations: Naming on Desmos
Yesterday we made names on desmos with points to create names. In the image above you can see my initials DY starting from x=0 and y=0
Now we magically used General form, Slope-y intercept form, and point slope form to re create the initials of our name. The top 4 is the D and the bottom 3 is the Y
Function Notation
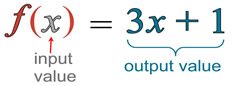
So in Function notation we use the input to find the output by using this equation. There are multiple ways to represent this including mapping notation.
So for say if the Input was 1 we would replace the x with 1. so 3*1=3
3+1=4 so when x=1 y=4
So every time X climbs, Y can climb with it. Or decrease depending on the question.
Functions and Relations

Today we were introduced into the universe of linear equations.
We learn that input is x and output is y
and several different possible use of an equation
f : x–> (0)x-1
f(x)=(0)x-1
As replacing the x in front of the f with a number then substituting the x in the equation gives us a problem to solve.
Solving this problem gives us Y
Final Chapter in Polynomials
We learned how to deal with the bad looking polynomials

When we look at this question, we see the coefficient 5. As the leading number. We see the y variable in the middle(just ignore that.)
We look for any common ground to divide.
If there’s none we look for difference of squares.
Then we move on to solving the question.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
There are multiple ways of solving math questions like this,
the one I prefer and that I sue is to get rid of the 5 then multiple the 5 to 7
x*2+2y-35
that way we have x*2 by itself, so then we realize that we can achieve 2 by 5 and 7 as it also gets 35
Polynomials: Factoring
Today we learned that as we can develop the question we must be able to do it backwards.
In this case we factored the question back to a simpler state. Solving this question is focusing on the 2x and the -5
I factor starting with 2 multiplying 5 making 10, then from 10 we determine how to get 9; which in this case is only 1 and 10 as its factors
so we put down (2x-1)(2x+10)
then simplying the 2 and the 10
=(2x-1)(x+5)
© 2025 Daniel's Blog
Theme by Anders Noren — Up ↑







