Lilo – Children’s Book
Reply
Author Archives: danielv-2014
Narrative Poem – La Luna – Daniel
Narrative Poem- Pixar Film- La Luna
A young boy at sea,
With his father and his grandpa making him at ease,
On a little white boat going into the breeze,
They hand him a gift wrapped in a cloth,
It’s a workers hat that is so soft,
His grandpa and his dad shape him like themselves,
As they adjust his hat and the little boy is puzzled,
Which side to choose to be his grandpa or his father,
They wait for the moon to come and that moment La Luna rises,
The boy grabs the anchor and is ready to climb,
Father sets the ladder and the little boy rises,
Reaching to the moon and setting his anchor,
The others follow setting foot in the sky too,
Stars scattered with a lot of work to do,
Father grabs the tools and proceeds to sweep,
The men of the family continue to fight,
Trying to shape the boy into what’s right,
Interrupted by a massive shooting star they take cover,
Something so absurd, they begin to wonder,
The men begin to try to pop the star out,
But fail again and again they begin to pout,
The little boy stares and thinks for awhile,
Choosing his own path his snaps his hat back.
He grabs his hammer and starts climbing the star,
As he reaches the top he gives the star a tap,
The star explodes into a thousand little ones now,
Grandpa and Father have never been so proud,
The little boy has finally found himself now,
He gets his own rake and shapes himself wow,
They continue their job and make their way back down,
As they reach their boat they look at their work,
They stare at the sky and see a crest moon,
La Luna is done the men are done to lurk
week 16- precalc
This week in precalc I learned the cosine law:
The Cosine Law :
c2 = a2 + b2 − 2ab cos(C)
Example: How long is side “c” … ?
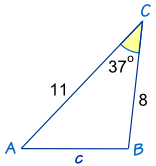
We know angle C = 37º, and sides a = 8 and b = 11
The Law of Cosines says:c2 = a2 + b2 − 2ab cos(C)
Put in the values we know:c2 = 82 + 112 − 2 × 8 × 11 × cos(37º)
Do some calculations:c2 = 64 + 121 − 176 × 0.798…
More calculations:c2 = 44.44…
Take the square root:c = √44.44 = 6.67 to 2 decimal places
Answer: c = 6.67
How to Remember
How can you remember the formula?
Well, it helps to know it’s the Pythagoras Theorem with something extra so it works for all triangles:
Pythagoras Theorem:
(only for Right-Angled Triangles)a2 + b2 = c2
(only for Right-Angled Triangles)a2 + b2 = c2
Law of Cosines:
(for all triangles)a2 + b2 − 2ab cos(C) = c2
(for all triangles)a2 + b2 − 2ab cos(C) = c2
So, to remember it:
- think “abc”: a2 + b2 = c2,
- then a 2nd “abc”: 2ab cos(C),
- and put them together: a2 + b2 − 2ab cos(C) = c2
When to Use
The Law of Cosines is useful for finding:
- the third side of a triangle when we know two sides and the angle between them (like the example above)
- the angles of a triangle when we know all three sides (as in the following example)
Example: What is Angle “C” …?
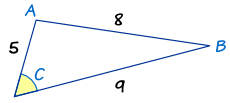
The side of length “8” is opposite angle C, so it is side c. The other two sides are a and b.
Now let us put what we know into The Law of Cosines:
Start with:c2 = a2 + b2 − 2ab cos(C)
Put in a, b and c:82 = 92 + 52 − 2 × 9 × 5 × cos(C)
Calculate:64 = 81 + 25 − 90 × cos(C)
Now we use our algebra skills to rearrange and solve:
Subtract 25 from both sides:39 = 81 − 90 × cos(C)
Subtract 81 from both sides:−42 = −90 × cos(C)
Swap sides:−90 × cos(C) = −42
Divide both sides by −90:cos(C) = 42/90
Inverse cosine:C = cos−1(42/90)
Calculator:C = 62.2° (to 1 decimal place)
Precalc 11 Week 15
This week in precalc 12 we learned about adding and subtracting rational fractions.
To add or subtract rational expressions with unlike denominators, first find the LCM of the denominator. The LCM of the denominators of fraction or rational expressions is also called least common denominator , or LCD. Write each expression using the LCD. Make sure each term has the LCD as its denominator. Add or subtract the numerators. Simplify as needed.
precalc 11 week 14
This week in precalculus we learned how to find asymptotes, to further explain I showed a few examples below:
In order to find the vertical asymptotes of a rational function, you need to have the function in factored form. You also will need to find the zeros of the function. For example, the factored function y=x+2(x+3)(x−4) has zeros at x = – 2, x = – 3 and x = 4.
If the numerator and denominator have no common zeros, then the graph has a vertical asymptote at each zero of the denominator. In the example above y=x+2(x+3)(x−4), the numerator and denominator do not have common zeros so the graph has vertical asymptotes at x = – 3 and x = 4.
If the numerator and denominator have a common zero, then there is a hole in the graph or a vertical asymptote at that common zero.
Examples:
1. y=(x+2)(x−4)x+2 is the same graph as y = x – 4, except it has a hole at x = – 2.
2.y=(x+2)(x−4)(x+2)(x+2)(x−4) is the same as the graph of y=1x+2,except it has a hole at x = 4. The vertical asymptote is x = – 2.
To Find Horizontal Asymptotes:
- The graph has a horizontal asymptote at y = 0 if the degree of the denominator is greater than the degree of the numerator. Example: In y=x+1x2−x−12 (also y=x+1(x+3)(x−4) ) the numerator has a degree of 1, denominator has a degree of 2. Since the degree of the denominator is greater, the horizontal asymptote is at y=0.
- If the degree of the numerator and the denominator are equal, then the graph has a horizontal asymptote at y=ab, where a is the coefficient of the term of highest degree in the numerator and b is the coefficient of the term of highest degree in the denominator. Example: In y=3x+3x−2 the degree of both numerator and denominator are both 1, a = 3 and b = 1 and therefore the horizontal asymptote is y=31 which is y=3
- If the degree of the numerator is greater than the degree of the denominator, then the graph has no horizontal asymptote.
Precalc 11 week 13
Graphing absolute value linear and quadratic equations:
1. Identify the vertex (not necessary for Linear functions). • Absolute Value functions: This is the point at which the definition of the function changes. Solve for the interval on which the expression inside the absolute value is greater than or equal to zero. • Quadratic functions: This can be determined from the standard form, y = b(x − h) 2 + k, and is the point (h, k). A Quadratic function can be written in standard form by completing the square. • Square Root functions: This can be determined from one of the two standard forms, y = b √ x − h + k or y = b √ h − x + k. Each Square Root function can only be written in one of the two standard forms. In either case, the vertex is the point (h, k).
2. Find the x-intercept(s), if any. For each type of function, this means solving the equation f(x) = 0. • Linear functions: There will always be exactly one x-intercept. • Absolute Value and Quadratic functions: There may be zero, one or two x-intercepts. • Square Root functions: There may be zero or one x-intercepts.
3. Find the y-intercept, if it exists. For each type of function, this means evaluating f(0). • Linear, Absolute Value and Quadratic functions: There will always be one y-intercept. • Square Root functions: There may be zero or one y-intercept.
4. Determine as many other points as needed (if any) to accurately sketch the graph. • Linear functions: We need two points in total. • Absolute Value functions: We need one point on each side of the vertex. • Quadratic functions: We need two points on each side of the vertex. • Square Root functions: We need two points other than the vertex.
5. Plot and label all of the points, and sketch the graph.
Precalc 11 – Week 12
This week we learned a lot about the substitution method.
The substitution method is most useful for systems of 2 equations in 2 unknowns. The main idea here is that we solve one of the equations for one of the unknowns, and then substitute the result into the other equation.
Substitution method can be applied in four steps
Step 1:
Solve one of the equations for either x = or y = .
Step 2:
Substitute the solution from step 1 into the other equation.
Step 3:
Solve this new equation.
Step 4:
Solve for the second variable.
Example 1: Solve the following system by substitution
Solution:
Step 1: Solve one of the equations for either x = or y = . We will solve second equation for y.
Step 2: Substitute the solution from step 1 into the second equation.
Step 3: Solve this new equation.
Step 4: Solve for the second variable
The solution is: (x, y) = (10, -5)
Precalc 11 week 11
This week in Precalc 11 we learned how to solve a quadratic inequality with one variable using a sign Chart.
The steps when using a sign chart is to:
1. Factor expression
2. Determine zeros
3. Use a sign chart for each factor
take this equation and make it equal to zero the factor —–> 5x > 2(x2-6)
Once you have factored determine the zeros (-3/2 and 4) and place them on two number line. Each number line will represent a different factor. One will be (2x+3) and one will be (x-4).
For each factor do a test point in all 3 sections. Pick a point less than -3/4, between -3/4 and 4, and greater than 4. Plug these test points in to the factor and determine whether the outcome is negative or positive.
Add up the positives and negative of the two number lines to determine what the equation will finally equal.Since the equation is asking for the equation to be less than zero we want x to be negative.
Week 10 Blog Post
3 things I learned this semester thus far:
The number in front the square root sign is the coefficient, the small number connected to the square root is the index and the number inside is called the radicand. We learned that the index is a very important clue for the equations because it tells us is the number in the radicand spot can me both negative and positive or only positive. Even number index can only be positive while uneven index can be either. Also simplifying equations, the index is important because it tells us what we can take out to become the coefficient. if the index is 2 we take groups of two.
Common Factors
Difference of Squares
Pattern
Easy
Ugly
C- Common Factor is when we look to find if the trinominal has something in common and if it does we will take it out so it makes our trinominal look more simple and easier to factor. For example in the picture below we need to recognize that we can take out a common factor of 3.
D- Différence In squares we need to see 3 things. Is it a binomial, is the refond term negative and, are they both perfect squares. If all of these are yes then we can factor it quite easily like in the example below.
P- Pattern is probably the easiest one because we are just checking if it has the right structure, and if it is then it is most likely facorable. Does it have X squared, does it have an X term and a number at the end. If yes then you can proceed to the next step.
E- Easy means if it is a easy polynomial to factor as in is does the X squared have a coefficient of 1. If it does this will be easy. Don’t stress until they are ugly.
U- Ugly is the opposite of easy (of course) which means that is the X squared has a coeficcisnt of 2 or more then it is considered ugly and you’ll have to do a bit more thinking.
completing the square-
probably the most complicated way to factor in my option because in order to do this process you need to move the third term and bracket the first 2. Then half the square the second term, the one inside the bracket will be positive and then one outside the bracket will be negative. Keep in mind if the first term has a coeficial you have to times the number by the coeficiant outside the bracket. To made this more clear I will show you a photo below.
week 9 blog post
This week in precalc we learned many things. We had to remember many things in order to successfully graph a quadratic equation.
- Convert between standard, general and factored form
- Standard form (vertex form) – vertex, line of symmetry, stretch value, opens up or down
- General form – y intercept (0,y), stretch value, opens up or down
- Factored form – roots (x- intercepts) (x,0), stretch value, opens up or down – > line of symmetry (find the average of the roots) ->the x value of the vertex
- ** factored form there needs to be integers rather than fractions
- a, p and q transform the graph
- a->stretch value, negative -> opens down, positive -> opens up
- A is a proper fraction 1/2 – compression – gets fatter
- A Is larger than 1 – stretch – gets skinnier
- P – horizontal translation (slide) (x-2) -> right (x+5) …. (x –5) -> left
- Q – vertical translation (slide) positive – > up negative -> down
- Maximum (opening down) and minimum (opening up) …. Vertex (y value or q)
- Standard graphing pattern … 1 3 5 …. So if a = 2 2 6 10
- Domain …all the values for x that you could plug into the formula …….
X E Real
- Range – all the possible y values y > minimum or y< maximum
- Completing the square – changes general form into vertex form
- Factor a trinomial …if it factors – nice roots
- If doesn’t factor …. Quadratic formula … discriminant …
- Table of values to graph
- Develop an equation from a word problem. modeling
These are key things in order to succeed in this chapter.