This week we started a new math unit on slopes and graphs. So far we have learned many things such as how to calculate the slope of a line, different slopes, different equations, and so much more. Two of the main things that I learned this week are the four different kinds of slopes and I also learned how to calculate a slope of a line that passes through two sets of given points.

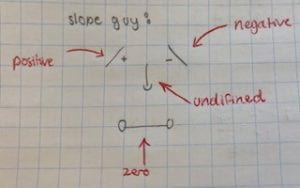
The four different kinds of slopes are positive, negative, zero, and undefined.

in class we learned about one method to help us identify whether a slope is either positive, negative, zero, or undefined. That method is called slope guy.

The next thing I learned was how to calculate a slope of a line that passes through two set of given points without using graph paper. You do this by finding the difference between them.

The two given sets of points that we’re going to use is (5,-1) and (-2,3)

First, we’re going to find the difference between the y values which are -1 and 3. That would be +4

Next, you have to find the difference between the x values which are 5 and -2. That would be +7

Lastly, you would turn it into a fraction and you always have to remember to make it so that it is always rise/run and y/x. because the difference between the Y values was 4 and the difference between the X values was 7 the fraction would be 4/7

Final answer: 4/7

One main thing we learned about this week was about graphs. We learned about how to find domain and range, we learned about finding out whether a graph is continuous or discrete, we got to find out whether it was a function or relation, and so much more.

This is the graph that we are going to be working with.

We are going to find its domain and range, find out whether it’s continuous or discrete, and lastly find out whether it’s a function or relation.

first: domain and range

The domain is the set of all possible inputs for a function. To find the domain, it can be shown on the X axis. That being said, the domain for this graph would be: -3 ≤ x ≤ 7

The range is the set of possible outputs. To find the range, you look at the Y axis. That being said, the range for this graph would be: -2 ≤ y ≤ 4

second: continuous or discrete

To find out whether the graph is continuous or discrete you look at the dots/lines. if there are just dots on the graph then it’s discrete. If the dots are connected and they form a line that it’s continuous. In this case, there is a line therefore this graph is continuous.

third: functions and relations

To find out whether the graph is a function or relation, you check to see if each of the input values leads to only one output value. If an input value has only one output value, then it is a function. But if it has two or more, then it is a relation.

You can also do a vertical line check to find out whether a graph is a function or relation period to do that, you can run a vertical line over your graph. If the line goes over two or more output values at once, then you’ll know immediately that it’s a relation and not a function. But if your vertical line goes over only one output value from the beginning to end of your graph then it is a function.

This graph passes the vertical line check so it’s a function.

 

In conclusion one main thing that I learned about this week was about graphs and how to find domain and range, find out whether it’s continuous or discrete, and to find out whether it’s a function or relation.

 

Factoring Polynomials

One of the main things that I learned about this week was about factoring trinomials.

I am going to go through the process of factoring simple trinomial step by step by referring to the factoring 123 method. But what is the factoring 123 method?

The factoring 123 method is where you:

1. First you have to find the greatest common factor of all the terms of the polynomial. This should always be done no matter how you are factoring or the kind of polynomial that you have (binomial, trinomial etc.)
2. Next you have to see if there are two terms and see if its a binomial. You have to see if there are a difference of squares.
3. The last step is to see if there are three terms which makes it a trinomial and factor it.

 

The first polynomial we’re going to factor is: x^2 + 10x + 24

This is a simple trinomial.

First you need to factor 24

2 x 12, 3 x 8, 4 x 6

Next you need to find factors that add to ten and multiply to 24

6 x 4 multiplies 24 and also adds up to 10

Now that you have found the factors you can put them into Two sets of brackets. There are two x’s, you put one in each bracket and then add a factor in each bracket. Your final answer will be:

(x+6)(x+4)

now to make sure we have the right answer we can check it. you multiply x by x then 4, then you multiply 6 by x then 4.

x times x, x times 4, 6 times x, 6 times 4

(x+6)(x+4)

X^2+4x+6x+24

Now you collect the like terms:

X^2 + 10x + 24

 

The next polynomial I’m going to factor is: 2x^2-20x

First you would factor out the greatest common factor which is step one of the factoring 123 method, find the greatest factor.

In this polynomial I would factor out the 2x and ill be moving the 2x to the front of the brackets

2x(           )

Now that you have two X in front of the brackets that would leave you with: x-20x

because you have 2x before the brackets you changed the -20 to -10 and put the x-10 in the brackets

that will leave you with: 2x(x-10)

 

Now you have to check your answer and see if you got it right by multiplying

2x times x, 2x times -10

2x(x-10)

2x^2-20x

We got the answer right.

In conclusion this week I learned about factoring polynomials.

Multiplying Binomials

One of main think that I learned about this week was multiplying binomials.

I am going to be using a method to help me multiply binomials. The method is called FOIL. FOIL stands for first, outer, inner, and last. First means that you multiply the terms that come first in each binomial. Outside means you multiply the terms that are on the outside of the binomial. Inner means you multiply the terms that are on the inside, and last means you multiply the terms in the binomials that are last of the binomials.

This is the equation that we are going to work with.

step 1. FOIL multiply the first terms in the binomials

first you multiply the first terms in the binomials and after you multiply them you get 35x^2

step 2. FOIL next you multiply the outer terms

second, you multiply the outer terms in the binomials and after you multiply them you get -30x

step 3. FOIL next you multiply the inner terms.

third, you multiply the inner terms in the binomials and you get 14x

step 4. FOIL lastly you multiply the last terms.

lastly, you multiply the outer terms in the binomials and you get -12

After you’ve multiplied all of the terms in the binomial you will end up with

Now all you have to do is collect all the like terms and you’ll end up with your final answer.

the final answer is 35x^2-16x-12

in conclusion, the main thing that I learned about this week was about multiplying binomials.

How to find an angle of a right triangle.

Exponent laws

One main concept that I learned about this week were the exponent laws: multiplication (product) law, division (quotient) law, and the power law.

Number 1: The first exponent law we learned was the multiplication law. This states that when you multiply 2 exponents with the same base, you keep the base and then add the powers.

=

step 1. multiply the bases

step 2. add the exponents

Number 2: The second exponent law we learned was the division law. This law states that when you divide 2 exponents with the same base, you keep the base and then subtract the powers.

=

=

step 1. subtract the x’s and y’s

step 2. re-write equations

Number 3: The third exponent law that we learned about was the power law. For this one, in order to raise a power to another power you need to multiply the exponents.

= × × ×

= × × ×

step 1. raise each factor to the power

step 2. evaluate the powers