FRACTIONAL EXPONENTS
 The denominator of the fraction exponent becomes the index, and the numerator stays as the exponent of the number. For example 4^3/2 you take the square root of 4 and multiply it 3 times by itself.
The denominator of the fraction exponent becomes the index, and the numerator stays as the exponent of the number. For example 4^3/2 you take the square root of 4 and multiply it 3 times by itself.
MULTIPLYING RADICALS
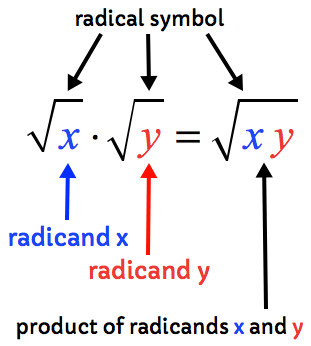 We can multiply radicals as usual like normal numbers by multiplying the RADICANDS, that is basically the final answer.
We can multiply radicals as usual like normal numbers by multiplying the RADICANDS, that is basically the final answer.
SOLVING INEQUALITIES
 (this is how it’d look on a number line)
(this is how it’d look on a number line)
Example: 3x − 5 ≤ 3 − x.
We start by adding both sides of the inequality by 5
3x – 5 + 5 ≤ 3 + 5 − x
3x ≤ 8 – x
Then add both sides by x.
3x + x ≤ 8 – x + x
4x ≤ 8
Finally, divide both sides of the inequality by 4 to get;
x ≤ 2
SINE LAW

The sine law allows us to find sides and angles much easier. The image above shows the sine law which is basically a (side)/sin A (angle) = b (side)/sin B (angle) = c (side)/ sin C (angle).
lets say we have a triangle where a = ?, b = 17, c = 3 and A = 93, B = 55 and C = 32
to find a, we’d use the sine law as shown:
COSINE LAW
We use Cosine Law to find the one side of a triangle if there are only 2 sides and 1 irrelevant angle given, if there are 3 sides given we can find an angle too.
For example, to find the a side, we square it and that basically equals the addition of the square roots of other sides, and then we multiply the sides and negative 2 and after that we find the cos of angle A and multiply it with that too. If we want to find the angle, we divide the equation to 2 parts. We first add the square roots of the sides and then subtract it from the square root of the side actual side and then we multiply -2bc and cosA , we divide the side by -2bc and then reverse the cos to cos-1 use it on the side, and after that we find the angle.

