on In my Edublog, I’ve added a background, changed the header fonts, added a theme, changed the menu, added a navigation bar (widget), a footer text, a video, a hyperlink and a quote. I’ve also changed the text color to blue-green. 
on This semester I displayed critical thinking in my midterm exam by getting %99 from it, and I also displayed responsibility by completing my edublogs.
on In history, we need critical thinking skills for almost everything. We have to analyze the data in front of us and make logical decisions. For example, Mikhail Gorbachev’s reforms. Most people in Russia argue that Gorbachev was a traitor for being one of the reasons why the USSR collapsed, while outside Russia, people see him as a hero for giving various rights to citizens. We have to analyze all the information given to us, ask important questions to ourselves whether Gorbachev did the right thing with the reforms (glasnost and perestroika) or not, and finally make a decision. This is why this assignment relates to critical thinking the most.
on FRACTIONAL EXPONENTS
The denominator of the fraction exponent becomes the index, and the numerator stays as the exponent of the number. For example 4^3/2 you take the square root of 4 and multiply it 3 times by itself.
MULTIPLYING RADICALS
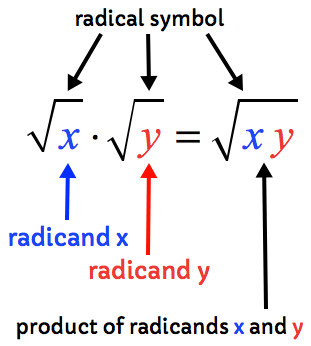We can multiply radicals as usual like normal numbers by multiplying the RADICANDS, that is basically the final answer.
SOLVING INEQUALITIES
(this is how it’d look on a number line)
Example: 3x − 5 ≤ 3 − x.
We start by adding both sides of the inequality by 5
3x – 5 + 5 ≤ 3 + 5 − x
3x ≤ 8 – x
Then add both sides by x.
3x + x ≤ 8 – x + x
4x ≤ 8
Finally, divide both sides of the inequality by 4 to get;
x ≤ 2
SINE LAW
The sine law allows us to find sides and angles much easier. The image above shows the sine law which is basically a (side)/sin A (angle) = b (side)/sin B (angle) = c (side)/ sin C (angle).
lets say we have a triangle where a = ?, b = 17, c = 3 and A = 93, B = 55 and C = 32
to find a, we’d use the sine law as shown:
COSINE LAW
We use Cosine Law to find the one side of a triangle if there are only 2 sides and 1 irrelevant angle given, if there are 3 sides given we can find an angle too.
For example, to find the a side, we square it and that basically equals the addition of the square roots of other sides, and then we multiply the sides and negative 2 and after that we find the cos of angle A and multiply it with that too. If we want to find the angle, we divide the equation to 2 parts. We first add the square roots of the sides and then subtract it from the square root of the side actual side and then we multiply -2bc and cosA , we divide the side by -2bc and then reverse the cos to cos-1 use it on the side, and after that we find the angle.
on We use Cosine Law to find the one side of a triangle if there are only 2 sides and 1 irrelevant angle given, if there are 3 sides given we can find an angle too.
For example, to find the a side, we square it and that basically equals the addition of the square roots of other sides, and then we multiply the sides and negative 2 and after that we find the cos of angle A and multiply it with that too. If we want to find the angle, we divide the equation to 2 parts. We first add the square roots of the sides and then subtract it from the square root of the side actual side and then we multiply -2bc and cosA , we divide the side by -2bc and then reverse the cos to cos-1 use it on the side, and after that we find the angle.
on 
The sine law allows us to find sides and angles much easier. The image above shows the sine law which is basically a (side)/sin A (angle) = b (side)/sin B (angle) = c (side)/ sin C (angle).
lets say we have a triangle where a = ?, b = 17, c = 3 and A = 93, B = 55 and C = 32
to find a, we’d use the sine law as shown:
on For distance, speed and time questions, we use a formula like this:
D is for distance, S is for speed, T is for time.
D = S.T, S = D/T, T = D/S
For motion problems, for example: if a current is 5 km/h, the upstream will be x-5 and the downstream will be x+5, x being the speed without current.
For proportion problems, for example if theres a mass of 12 kg of a substance and if we want another substance to be %40 of the mixture, we use x/x+12 = 40/100.
on To cross multiply rational expressions, there has to be one monomial in the left side of the equation and another monomial in the right side of the equation. For example, in this equation, we multiply 5 and x+4, as well as 3 and 6. This becomes 5x + 20 = 6. 5x = -14. x = -14/5 
on
Example: 3x − 5 ≤ 3 − x.
We start by adding both sides of the inequality by 5
3x – 5 + 5 ≤ 3 + 5 − x
3x ≤ 8 – x
Then add both sides by x.
3x + x ≤ 8 – x + x
4x ≤ 8
Finally, divide both sides of the inequality by 4 to get;
x ≤ 2
This is how it’d look like on a number line.
on y = a(x – p) squared + q
a is the stretch, if it is positive, the parabola is looking UPWARDS. The p decides which way the vertex moves. If it is positive, it moves to the LEFT. If it is negative, it moves to the RIGHT. The q is the y intercept, so if it is positive, the vertex moves UP. If it is negative, it moves DOWN.