In Grade 9, we looked at the concept of grouping like terms.
Grade 9; 5x + 6y – 3x + 9y + x
x = 3x
y= 15y
Now in Grade 11, we now group radicals.
Grade 11; 4![\sqrt[3]{9} \sqrt[3]{9}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B9%7D&bg=ffffff&fg=000000&s=0) , 6
, 6![\sqrt[3]{9} \sqrt[3]{9}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B9%7D&bg=ffffff&fg=000000&s=0) , 15
, 15![\sqrt[3]{9} \sqrt[3]{9}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B9%7D&bg=ffffff&fg=000000&s=0)
= 25![\sqrt[3]{9} \sqrt[3]{9}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B9%7D&bg=ffffff&fg=000000&s=0) .
.
Rule
Radicand and index must be the same.
Subtraction
 –
– 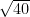
=  –
– 
= 4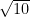 – 2
– 2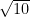
= 2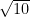
Division and Multiplication Rule
The denominator CANNOT be a radical
Rationalizing the Denominator
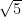 / x
/ x  =
=  / ——->
/ ——->  /
/
 x
x  =
=  ——-> 6
——-> 6
Rationalizing the denominator is a way of cancelling out the radical so the denominator is not a radical.
1.) Recognize that the denominator is a radical
2.) Multiply both the numerator and the denominator (what you do the bottom you got to do the top)
3.) Simplify to find the new values
4.) See if there are any perfect squares (if the index is for example 3, then look for perfect cubes)
5.)Simplify the new values
6.) MAKE SURE A RADICAL IS NOT IN THE DENOMINATOR PLACE.



