This week in Math 10, I have chosen to talk about polynomial models.
To begin, polynomials are essentially the language of mathematics. For the purpose of this article, a polynomial is a series of terms (variables, coefficients and standalone constant numbers) connected by + and – signs, with groups of terms being created using brackets, which count as a single term. For example…
(4x+2)(3x-5) (The lack of a symbol between brackets is considered a multiplication)
Modelled, this polynomial (more accurately, a binomial, due to the number of terms) looks like this.
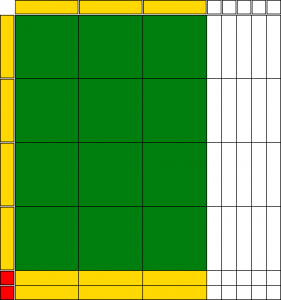To explain what you’re seeing, the coloured shapes are positive, and the colourless tiles are negative. Small squares represent 1, rectangles represent x, and large squares represent 
Along the top and left borders of the image are representations of the polynomial previously stated, with 4x+2 to the left and 3x-5 on top. All the other shapes are representations of the result of multiplying the original polynomial. The positions of the original polynomial terms between the two positions do not matter, so long as they are accurately represented.
It represents the polynomial
Notice how the large squares are concentrated near the original x rectangles, how the x rectangles on the bottom are horizontal as opposed to vertical, and how the single units are concentrated in the opposite corner to the originals.