What is an equation?

An equation is a statement of equality using variables, comprised of 2 expressions connected by an equals sign. An example:

3x+4=x-6

The above equation is expressing that 3 times the variable plus 4 is equal to the variable minus 6.

Equations can contain fractions and decimals, like so.

+5.2=

Return to top of page

What are equivalent equations?

An equivalent equation is a “simplified” version of an equation, created by removing or adding an amount to both expressions. For example:

9x+2=2x+6

Subtracting 2 from both expressions…

9x=2x+4

That is an equivalent equation.

Return to top of page

How to solve equations

To solve an equation, there are two methods that I have learned.

• Using algebra tiles
• Algebraically

I will start with algebra tiles.

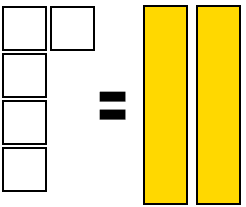
This is the equation 4x-4=6x+1 depicted with algebra tiles.

To solve the equation, we must do legal moves. Legal moves are operations that can be performed on both expressions. For example, we can subtract 4 positive rectangles, and it would be legal. We cannot, however, subtract 4 negative squares, but we can add 4 positive squares, nullifying the 4 negative squares, which would be zero pairs. This is the equation if 4x is subtracted.

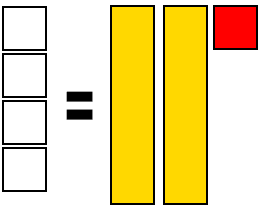We can now add one negative square, as the variables are on the right side, and we need to simplify the right side to the rectangles. This is isolating the variable.

At this point, we can divide each expression by the number of variable rectangles, which is in this case, 2.

-5 2 = -2.5

x= -2.5

Solving algebraically is very similar to solving polynomials, and still uses the method of legal moves. Solving algebraically is ideal for equations containing fractions, decimals or coefficients. An efficient order to solve algebraically is brackets, fractions, sort, divide. As an example, I will demonstrate solving an equation with fractions, decimals and coefficients.

First, as is equal to , we will replace it with We will also convert 2.5 to and 1.2 to . While not required,

Then, we distribute 3, multiplying and -0.4.

We change to have a common denominator with

At this point, we now begin to cut down the equation. We’ll start by subtracting

Now, we’ll subtract 2.5.

We can determine that x=-11.1 by multiplying it by 3, as -3.7 is one third of x.

Return to top of page

How to verify if a solution is correct

To verify an equation, one would replace the variable with its supposed value and effectuate the equation as is. If the two expressions equal the same value, then the equation is correct. For instance, I will use 4x-4=6x+1 from my algebra tiles example. The supposed solution was -2.5, which means the new equation is -10-4=-15+1

-10-4=-14

-15+1=-14

This confirms that the solution is correct.

Return to top of page