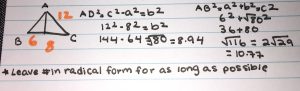Math 10 Honours Numbers Summary
Over the past few weeks, our class has done a lot of work around numbers and radicals.
Numbers and Prime factorization:
We talked about the real number system something that I am quite familiar with, as well as what makes up numbers. We learnt if a number only has two factors one and itself it is prime and that if it has any more factors than that it is composite. These are things I was already aware of but the interesting things in this lesson were the fact that 1 and 0 are not composite or prime because they both have less than two factors. The absolute value of a number is their principle square root. Another new concept was prime factorization which is when you break down a number to make it a product of only there prime factors.
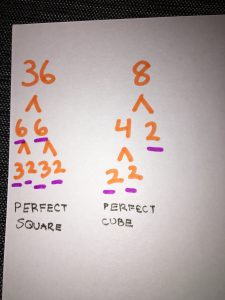
In this example, we broke down 36 into two numbers 18 and 2 then separate 18 into 2 and 9 and then 9 into 2 and 3. Which leads the prime factorization to 2 x 2 x 3 x 3.
With that, we learnt how to find the greatest common factor of multiple numbers by finding the common numbers in their prime factorizations and multiplying them together.
You can also find their lowest common multiple in a similar process by finding their prime factorizations and multiplying all the numbers that they each are made up of except for the similar ones in which case you only multiply them by that number once.
We learnt that in prime factorization if the factors occur in twos the number is a perfect square and if they occur in threes then the number is a perfect cube.
We talked about what makes a number rational or irrational and since a repeating decimal is rational, we learnt how to turn them into fractions so that they fit the definition of a rational number.
Radicals:
We learnt what makes up a radical. If there is no index written, we assume that it is 2. We learnt the radical laws, how you can multiply and divide radicals to put them under the same radical sign. But you cannot add and subtract radicals.
This is how exponents with a higher index work, which was also a new concept to me.
We learnt the difference between a pure/entire radical and a mixed radical. How to convert an entire radical to a mixed radical. This is important for reducing your answers. I learnt that leaving a number in radical form for as long as possible is crucial to get the closest exact answer possible.
You can also change mixed radicals into entire radicals by dividing the coefficient by raising the coefficient to the power of the index. And then multiplying your answer with the number that is already under the radical sign.
Examples of how you can apply radicals in math
We also learned how to convert variables that are in entire fractions into mixed fractions. With the first example down a to the 7 by finding a number that is divided by two and then subtracting that number from 7 which is the exponent law of adding exponents with the same base to multiply. Then you divide that number by the index which in the first case is 2. Then you are left with a to the 3 outside of the radical sign and a to the 1 inside the radical sign. Underneath that are a couple more examples.