With this being the last blog post of Precalculus 11, I want to talk about 5 things I learned in this class that have been enjoyable or eye-opening.

Sine law & cosine law

• these 2 laws have to be one of the most interesting things I learned this year because they took everything that I learned in Math 10 and summed it up into formulas. This is way easier to use than SOH CAH TOA or anything similar.
• here are the formulas

• Sine Law: Useful for finding unknown sides or angles in non-right triangles when we know either:
  • Two angles and one side
  • Two sides and a non-included angle
• Cosine Law: Useful for solving triangles when we know:
  • Two sides and the included angle
  • All three sides to find any angle

Quadratic formula

• this formula is another example of a formula that I could’ve used in math 10 to make math a little easier. once you have the formula memorized it becomes a straightforward process to apply it to any quadratic equation and compared to other factoring methods like completing the square or grouping, this is way more straight forward.
• here is the formula 
• once you have identified your values and put them in the formula you start solving for x
• by only solving the discriminant you can find the nature of the roots
• if discriminant = 0 —- there is 1 solution
• if discriminant = negative —– no solution
• if discriminant = positive —– 2 solutions

Radicals as powers (flower power)

• viewing radicals as fractional exponents makes working with them a lot easier. once you apply the radical as a power you can easily apply all the exponent rules to the expression.
• the denominator is the root.
• the numerator is the power 

Graphing quadratic functions

• graphing quadratic functions provides a visual representation of the relationships between variables. it shows how many units the parent functions needs to move around.
• The graph of a quadratic function is a parabola, which is a U-shaped curve. The direction and openness of the parabola depend on the sign of the coefficients. If a > 0, the parabola opens upwards, and if 0>a the parabola opens downwards.

• Vertical Translations: Adding a number moves the graph up. Subtracting a number moves the graph down.
• Horizontal Translations: Adding a number inside the function shifts the graph left. Subtracting a number inside the function shifts the graph right.
• Vertical Stretching/Compression: Multiplying the function by a number: If the number is greater than 1, it stretches the graph vertically. If the number is between 0 and 1, it compresses the graph vertically

Restrictions with radical

• the last thing is the restrictions that come with radicals and even fractions. restrictions ensure that we have real number solutions and that the solution is not undefined/no solution.
• Even-Root Radicals (e.g., Square Roots):
  • The radicand (the number under the root) must be non-negative. This is because the square root of a negative number is not defined in the real number system (it belongs to the complex number system).
  • For example, square root of x, $x\ge 0$.
• Odd-Root Radicals (e.g., Cube Roots):
  • The radicand can be any real number (positive, negative, or zero). This is because the cube root of a negative number is a negative number, and the cube root of a positive number is a positive number.
  • For example, cube root of x, all real x. 

This week in precalc 11 we learned about sine law. I chose this topic to cover for this week because you can use sine law for any type of triangle (acute, obtuse, right, non-right etc.) you can also use this formula to find angles AND sides. 

If you would like to find an angle, have SIN be on top. If you want to find a side flip it the other way (small letter goes on top)

• once you have the formula fill it out with the given information.
• Sin A, B, C are the angles
• a, b, c are the sides
• Select one of the ratios from the law of sines based on the given parts of the triangle.
• Use the chosen ratio to set up an equation involving the known and unknown parts of the triangle.
• isolate and solve.
• make sure to add brackets when putting the numbers in the calculator.

In trigonometry, special angles have exact trigonometric values, which are useful for simplifying calculations and solving problems. The special angles are 30°, 45°, and 60°.

30°/60°Angle

Reference Triangle: The 30° angle is often found in a 30°-60° triangle, which is half of an equilateral triangle.

45° Angle

Reference Triangle: The 45° angle is found in a 45° triangle, which is an isosceles right triangle.

• In a 45° triangle, both legs are equal in length.

Use this concept whenever you get a reference angle of 30,60 or 45. make sure to draw the triangles and refer to them throughout the question. use the x,y and r values given by the triangles.

Problem: Find the exact values of sin⁡(150°), cos⁡(210°), and tan⁡(330°)

$sin\; (150°)$

1. Reference Angle: 180°−150°=30
2. Trigonometric Value: sin 30° = y/r —> square root of 3/2 

$\cos (210°)$

1. Reference Angle: 210°−180°=30 
2. Trigonometric value: cos 30°= x/r —> 1/2

$\tan (330°)$

1. Reference Angle: 360°−330°=30°
2. Trigonometric Value: tan⁡(30°)= y/x —-> 2 

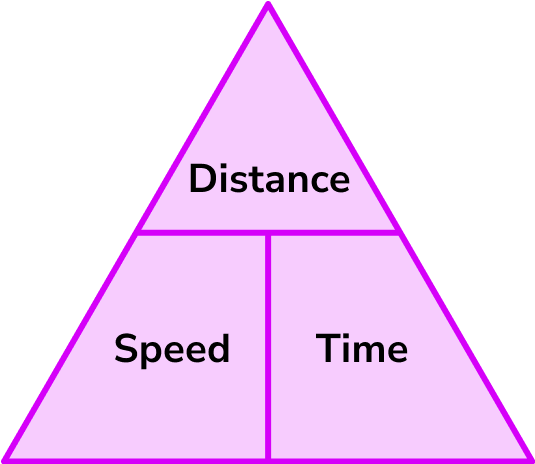This week in Pre calc 11 we have been working on rational expressions. I learned how to tackle word problems with rational expressions this is useful because many of these word problems are problems that you would tackle in the real world. I’m going to be talking about distance, speed and time problems. To get started we need to memorize this formula that can help us solve:  if you want to find speed, you cover speed with your finger and see that distance is on top of time, this means that we need to divide distance over time to figure out speed. The same goes for the rest.

World Problem:  Evan drove 308 km at the same time that Meghan drove 329 km. If Meghan drove on average 6km/h faster than Evan, calculate her average speed and the time taken for the journey. 

step 1. Read the questions carefully and figure out what you are trying to find. We are trying to find Meghan’s speed.

step 2. Make a let statement. This word problem doesn’t tell us the time, it only tells us that Meghan was 6km/h faster. Therefore let x be Evans speed.

step 3. Draw your table and plug in numbers

step 3. time. to find the time, we use our triangle. Distance divided by speed. the only information given about time is that Mgehan and Evan drove in the same time. This indicates that our expressions would equal one another.

step 4. solve the equation.

Step 5. add 6 because meghan was 6km/h faster

This week in precalc 11 we learned how to add, subtract, multiply and divide rational expressions. In this unit, rational expressions are complex-looking fractions with variables. I will be focusing on how to multiply these rational expressions

Working with rational expressions is no different than working with regular fractions. In regular fractions, we multiply across and simplify where possible.

Example: 

• simplify
• multiply across
• set restrictions (non permissible value)
• cancel things out

Example:

• factor if possible
• cancel things out
• multiply
• set restrictions
• bring down the other expression and do the same

This week in precalc we started working with rational expressions (fractions with variables). We first started with simplifying them which is a key aspect for working with these kinds of questions (adding, subtracting, etc.). It is important to remember after each question you are required to state the non-permissible value because there is a variable in the expression.

Non-permissible value: The value of a variable that makes the denominator of a rational expression equal to zero.

example 1:

• the first thing should always be observing to see if you can make the expression any simple like factoring out anything or cancelling any numbers or variables.
• In this case, we can cancel (a-8).
• The non-permissible value should always be stated before you cancel anything out.

example 2:

• by observing the expression we can see that both the numerator and the denominator are factorable.
• write the non-permissible value
• cancel anything that is left over.

example 3:

• here we can see that the expressions are similar but they aren’t in the same order.
• in this case, we can still simplify BUT it does not simplify to a 1. It simplifies to a -1.

This week in Precalculas 11 we went over inequalities and what they mean. We also learned how to graph them. In graphing inequalities, we can use what ve learned from the last unit, like vertex, x-intercept, y-intercept, etc. to help us graph inequalities.

Example : y> – (x+4)^2

• first I graphed the expression on demos without the inequality sign to see what it would look like. in this example we already have the inequality in vertex form so it is easy to graph but if we dont have to solve it a little bit.

• now that I plugged in the inequality sign there are some changes we can see so let’s break it down

1. As you can see the parabola has a dashed line, this is because our inequality does not have the small line under it. This means that y is greater than… If it was greater than or equal we would but a bold line.
2. Everything outside the graph is shaded. This is because of the inequality sign. Our expression is telling us that our solution has to be greater than – (x+4)^2. So how to we figure out where to shade.

• take a random point in a graph and plug in the x and y into the original function
• if you get a true statement then this means that the shading should go in this zone. In this case it is outside the parabola. 
  

This week in pre-calc 11, we briefly went over inequalities and systems in one lesson. By inequalities, I’m referring to the relationship between two expressions. I like to think about the inequality signs as alligator mouths, they eat whichever number or expression is the biggest.

example: x>7 — x is bigger than 7 that’s why it is getting eaten. X could be any number that is above 7

example: 78 x —– x is bigger than or equal to 78.

• during graphing or on number lines if there is a dash line, it means the inequality sign does not have the small line under it

• if there is a solid line, it means that the small line is on the inequality sign.

Graphing inequalities :

• When the expression is given to us, we move everything to one side and make sure to isolate y. what we are left with is our slope and y-intercept.

• graph the expression
• the inequality sign tells you which side of the line to shade, to figure this out take point (0,0) substitute into the inequality and simplify. If the inequality is false we shade the part that doesn’t contain the point.  if it is true we do shade the point.

General form – Ax + By + C = 0 

Vertex form – Y = a (x-p)^2+ q

Example: y=3x^2+18x+20 

Step 1: Factor out the leading coefficient. Steps 2 & 3: Complete the square, at the same time as completing the square multiply the number that is not part of the equation by the coefficient

step 4: simplify

This week in Precalc 11 we started the intro to quadratic functions. The graph of a quadratic function is a parabola, which is a U-shaped curve. The direction and openness of the parabola depend on the sign of the coefficients. If a > 0, the parabola opens upwards, and if 0>a the parabola opens downwards.

Vocabulary :

parent function:

• the parent function spacing follows the 1 – 3 – 5 – 7 … pattern
• y=x^2 
  

Vertex: the turning point of the parabola (also known as the most important point on a parabola)

Maximum of quadratic function: the highest point on a graph when a parabola opens down

Minimum of quadratic functions: the lowest point on a graph when a parabola opens up

The axis of symmetry: the equation of a line that divides the figure into two equal parts where one is the mirror image of the other.

The standard form: 

• Vertical Translations: Adding a number moves the graph up. Subtracting a number moves the graph down.
• Horizontal Translations: Adding a number inside the function shifts the graph left. Subtracting a number inside the function shifts the graph right.
• Vertical Stretching/Compression: Multiplying the function by a number: If the number is greater than 1, it stretches the graph vertically. If the number is between 0 and 1, it compresses the graph vertically

Here is an example:  f(x)= (x-2)^2+3

The blue parabola is the parent function, and the green parabola is the example. In the green parabola we can see that the minimum value is y=3 but in the blue parabola it is 0. this is because in the equation we have a vertical translation of +3 this made the parabola move up 3 units. Another difference is that the green parabolas axis of symmetry is at x=2 rather than 0. Again this is due to the horizontal translation. Even though it says -2 in the brackets we are moving to the right when a negative sign is seen. If a positive sign is seen in the brackets we move to the left.