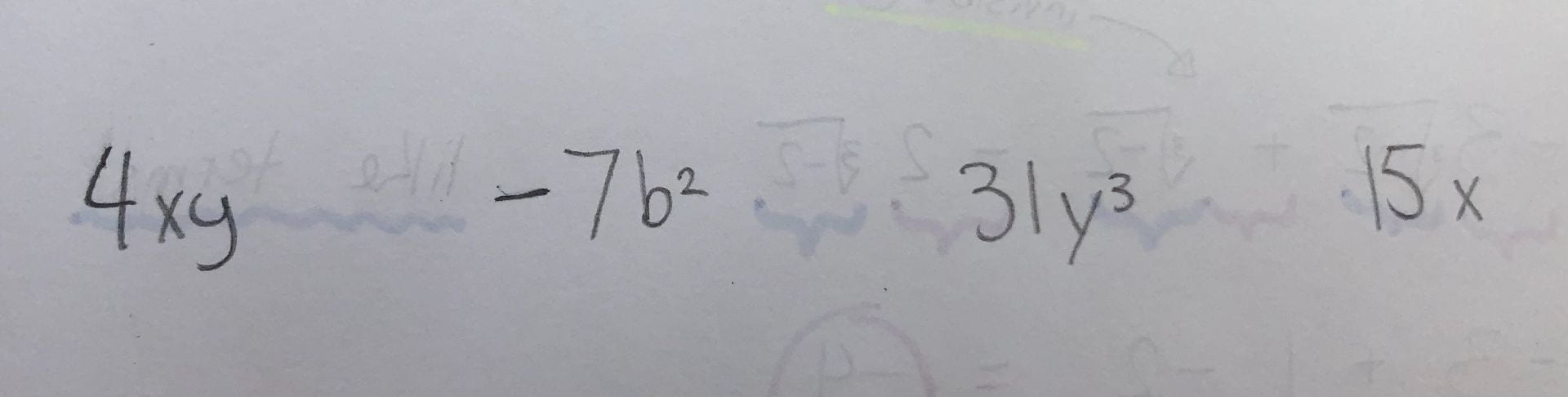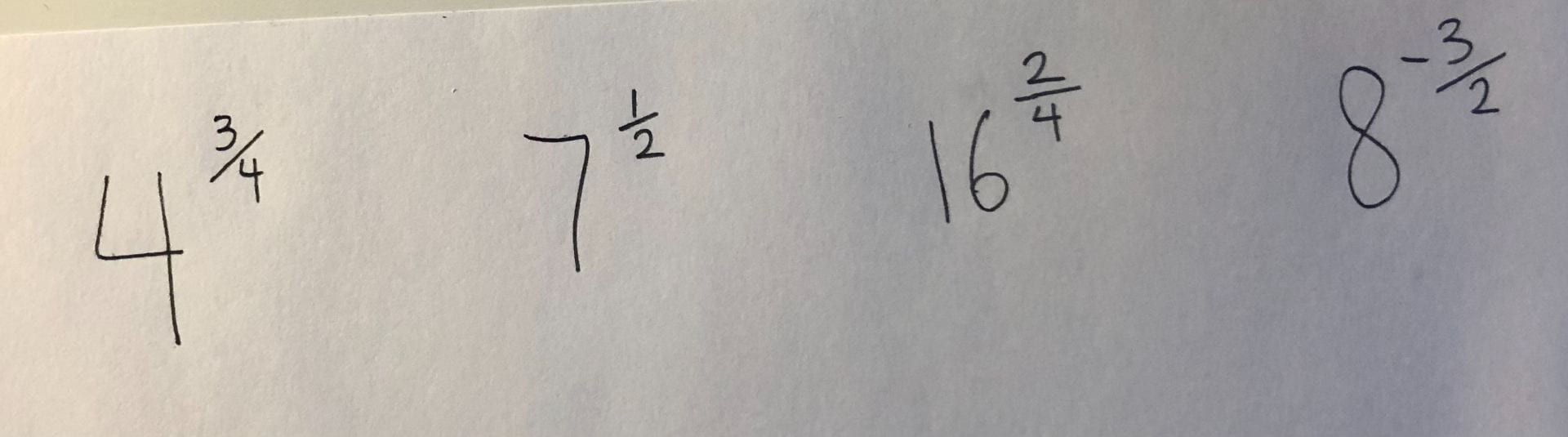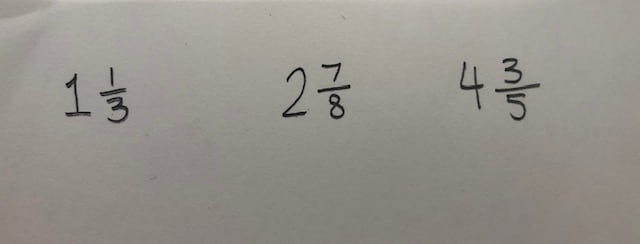In precalc 11 class this week, we learned about adding and subtracting radical expressions. This involves combining like terms that are radicals. Like terms is something I had learned about before, but I didn’t realize it was possible with radicals. Terms are numbers, variables, and/or exponents in groups. Here are four examples of terms:

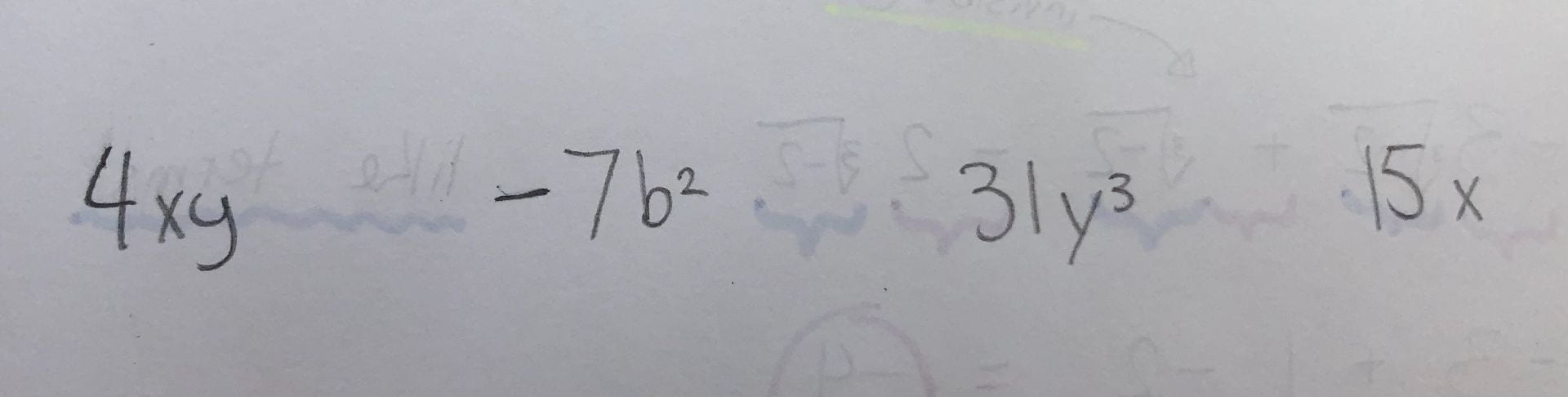
When the variables and exponents in more than one term are the same, the terms are “like”. The coefficients (number in front of the variable) can be different. For example:

When multiple radicands and their index are the same, they can be combined. For example, these radicals are like terms, because they have the same radicand and index (the square root of 4):

It is important to remember that the coefficient can be different for each term, because that is what’s being combined. To combine like terms, add/subtract the coefficients based on the sign in front of them. If there is no sign, it is positive. Here are the steps to combine like terms that are radicals:

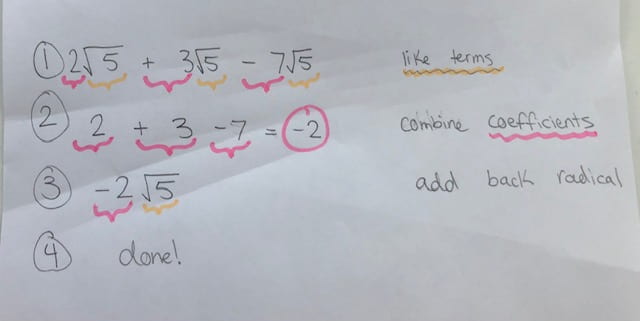
If the radical has no number in front, there is an invisible coefficient of 1. Don’t forget to add or subtract it as well! Here is one final example:

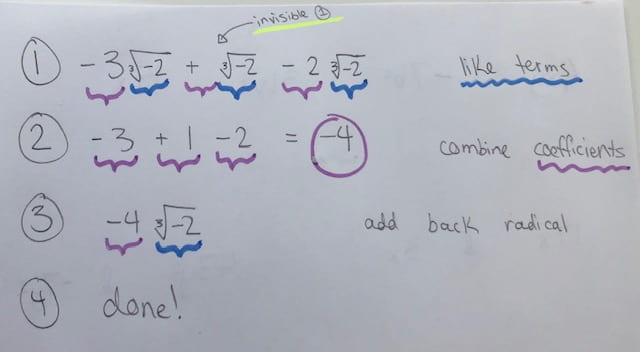
This week in precalc 11, I learned how to evaluate an exponent that is a fraction. In the textbook, this is known as “writing powers with rational exponents”. Since all fractions are rational numbers, it is possible to make fractions into exponents on numbers. Here is an example:

Below are some other examples. As you can see, the fraction can be positive or negative:

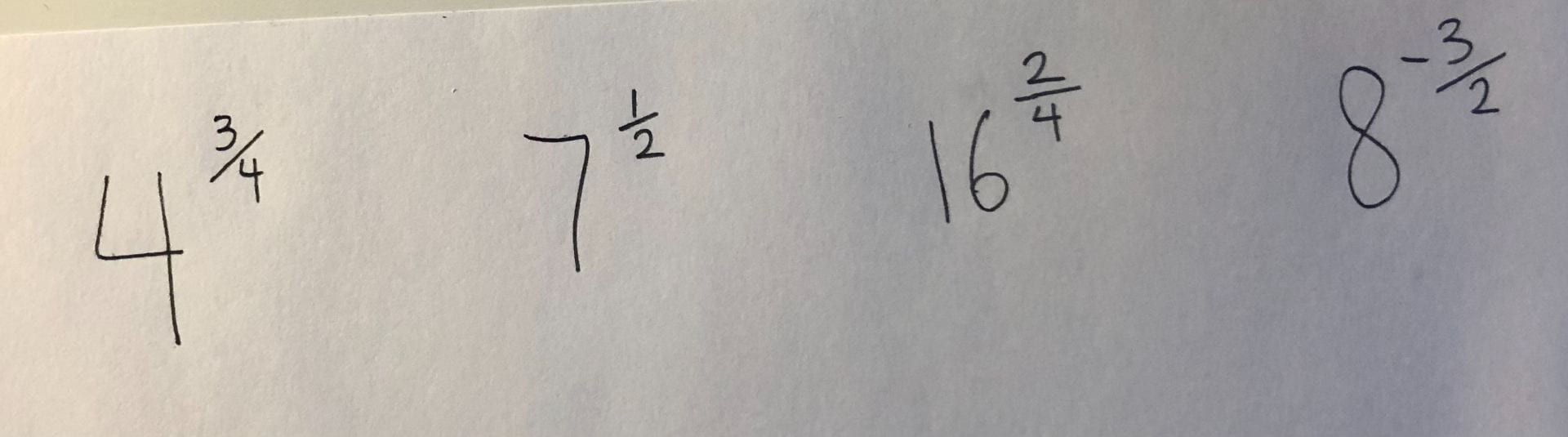
To solve a fractional exponent, you change the base number from being a power, into a radicand within a radical. In my class I learned the saying “flower power, because the root is always on the bottom”. This is a helpful way to remember that the denominator (or bottom number) in the fractional exponent becomes the index in the radical.

This example below demonstrates the steps of changing a number with a positive fractional exponent into a radical. The numerator (top of fraction), can be placed as the exponent either on just the radicand, or the entire radical. I prefer to do it whichever way makes the numbers easier to solve. After this is done, the radical can be further evaluated.

This example shows the same steps, with a negative exponent. There are different ways to do this, but I chose the one I like best:

This week in Pre-calculus 11, I learned about roots and powers. Something I hadn’t learned about before were mixed radicals, and how to create one from a regular radical. A mixed radical is similar to a mixed fraction, where there is a whole number and a fraction together. Here are some examples of mixed fractions:

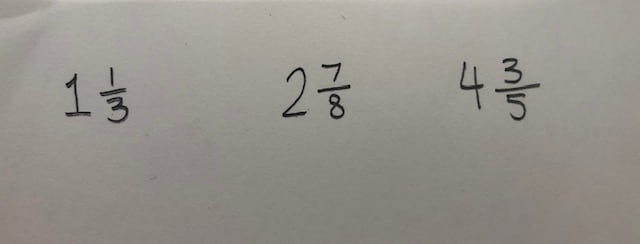
A mixed radical looks like the photo below, where there is a number inside the square root sign, as well as a number outside:

To change a radical from being entire (only a number inside the square root sign) to mixed, you can follow the steps below. In step 2, make sure one of the numbers is a perfect square (9, 25, 49, etc.)

To change a radical from mixed back to entire, follow the steps below. In step 2, don’t forget to add the outside number in twice. This will make sure you multiply it by itself, so it becomes a perfect square number.

Here are two more examples: