

This week we learned how to solve/ use algebra tiles in an equation. we have used blocks and tiles ever since we were younger and now is the time that algebra tiles get more complex. I did struggle with converting algebra tiles into an equation but once I learned I got the hang of it. there is still more room for improvement in this area of our polynomials unit.
when given algebra tiles to convert into an equation you should…
- determine that shaded tiles = positive and not shade tiles = negative
- know that the biggest tile (x² tile) = x², the skinny long tile (x tile) = x , and the smallest tile (1 unit tile) = 1
- figure out which tiles you have and determine whether they are positive and or negative
- in this case, we have a negative (x² tile), a positive 2 (x tile), and a positive (1 unit tile)
- we only have 1 negative (x² tile) this will equal -x²
- we have positive 2 (x tile) so this will equal +2x
- and we know we have 1 positive (unit tile) this will equal +1
- know we put it all together so it will = -x²+2x+1
- and this will be vis versa if you were given -x²+2x+1 you would be able to convert it into tiles because you know how many tiles there are, and what is positive and negative.
I chose this topic during our polynomials unit because I did struggle with this as I found it difficult for myself to convert the equation into tiles. I do understand this concept a lot more than I used to, but I still think that for more complex questions I could use more practice to be prepared for tests and just personal knowledge. I think learning about algebra tiles is important as we have basically been using them all of our lives. this post hopefully can help others who are misunderstanding and also be a guide for me when I am struggling or forget how to solve these types of questions. I have learned that when solving bigger equations and converting them into tiles they can look something like this: 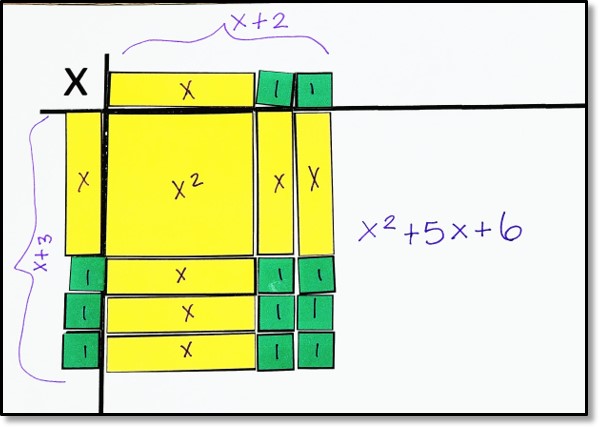
I didn’t realize that I should’ve been expressing te equation lie this and not all in separate squares.
citations: