This week I learned how to estimate the number value of two radicals (an expression containing a square root) that may not be a perfect square, perfect cube, or perfect fourts. In previous learning, evaluating square roots was exclusivly evaluating perfect squares such as  which as we know is equal to 5, because
which as we know is equal to 5, because  in other terms is symplifying 5 to the power of it’s self. This week in math I was introduced to evaluating perfect cubes, such as
in other terms is symplifying 5 to the power of it’s self. This week in math I was introduced to evaluating perfect cubes, such as ![\sqrt[3]{27} \sqrt[3]{27}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B27%7D&bg=ffffff&fg=000000&s=0) which is equal to 3, because the cube root of 27 is the number which when multiplied by itself three times gives the product as 27, since 27 can be expressed as 3 × 3 × 3. Therefore, the cube root of 27 = ∛(3 × 3 × 3) = 3. We have also looked at perfect fourths such as
which is equal to 3, because the cube root of 27 is the number which when multiplied by itself three times gives the product as 27, since 27 can be expressed as 3 × 3 × 3. Therefore, the cube root of 27 = ∛(3 × 3 × 3) = 3. We have also looked at perfect fourths such as ![\sqrt[4]{16} \sqrt[4]{16}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B16%7D&bg=ffffff&fg=000000&s=0) which is equal to 2 (
which is equal to 2 (  ). But what happens when you need to estimate the value of a radical that is not a perfect square, cube, or even fourth?
). But what happens when you need to estimate the value of a radical that is not a perfect square, cube, or even fourth?
These are the steps to go about it…
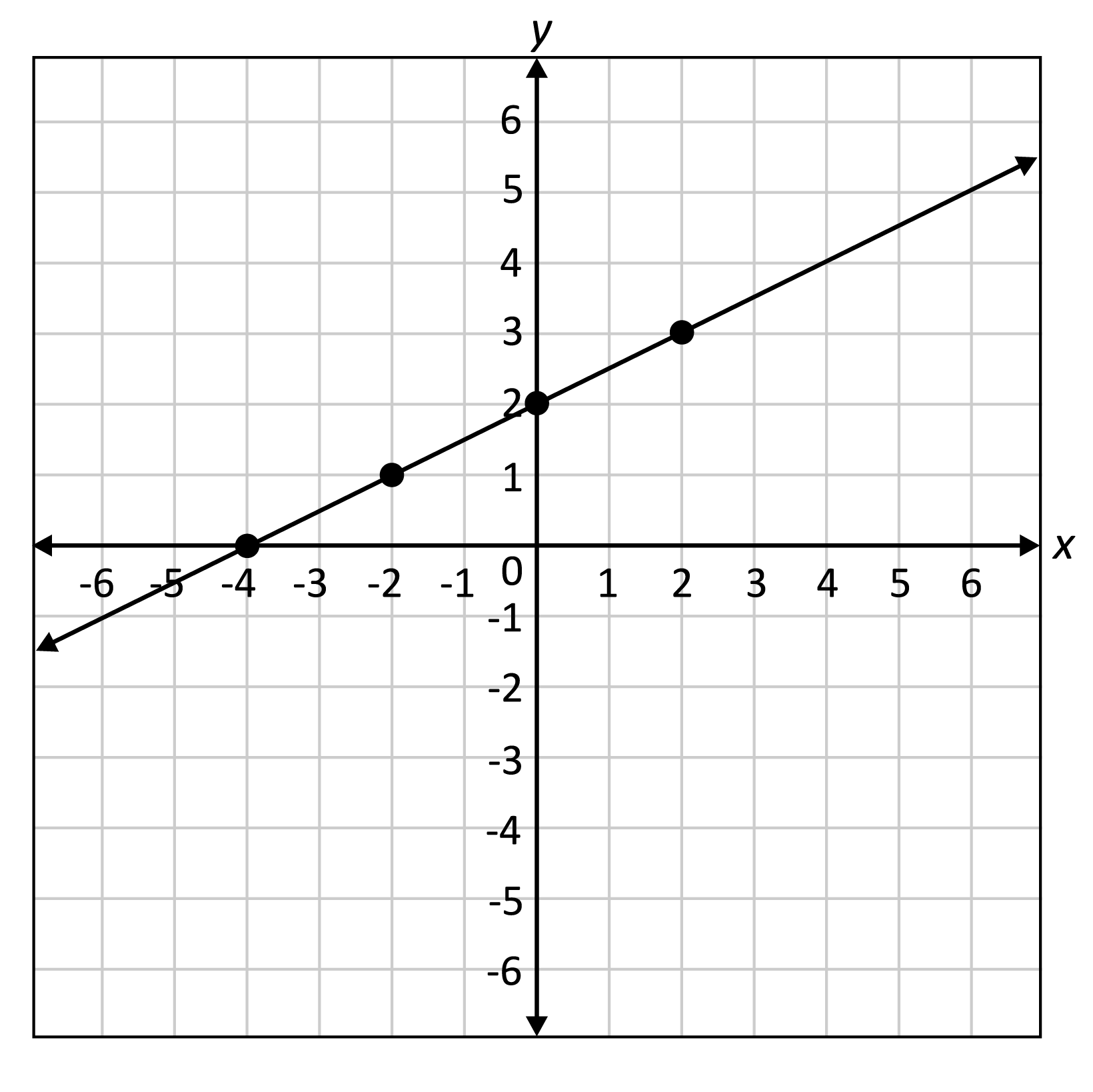
In the first example I am evaluating the cube root of 20, which is not a perfect cube. Therefore, the next best way to evaluate this cube root is to estimate it’s value to the nearest tenth, using what knowledge we have about perfect cubes. This is a crutial skill to have, as throughout pre calculus 11, evaluating radicals without a calculator is a re-occuring concept. Furthermore, I chose estimating the value of radicals as my subject for this week’s post because in the past I have struggled with understanding radicals as well as making mathematical estimations; however, I feel more comfortable now due to the homework we completed in class.

Further explanations of the steps from example 1.
Step 1- After memorizing the first 10 perfect cubes, I was able to recognize that 20 is not a perfect cube, and I must find the two perfect cubes 20 falls between in order to make an estimation on it’s value.
Step 2- I made the connection that 20 falls in between the two perfect cubes 8 and 27.
Step 3- I calculated the difference between 20 and 8 and 27 and 20. The cube root of 27 was closest to 20 which would mean my value has to be closer to ![\sqrt[3]{27} \sqrt[3]{27}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B27%7D&bg=ffffff&fg=000000&s=0) , which after evaluating we know that
, which after evaluating we know that ![\sqrt[3]{27} \sqrt[3]{27}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B27%7D&bg=ffffff&fg=000000&s=0) = 3, and
= 3, and ![\sqrt[3]{8} \sqrt[3]{8}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B8%7D&bg=ffffff&fg=000000&s=0) = 2, in other terms
= 2, in other terms ![\sqrt[3]{20} \sqrt[3]{20}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B20%7D&bg=ffffff&fg=000000&s=0) falls between 2 and 3 but is closer to 3.
falls between 2 and 3 but is closer to 3.
Step 4. I know that my value is closer to 3 but cannot surpass it, so my educated estimate would be ![\sqrt[3]{20} \sqrt[3]{20}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B20%7D&bg=ffffff&fg=000000&s=0) ≈ 2.7
≈ 2.7
Example 2.

Further explinations of example 2
In this example I chose a value that was a bit larger, the square root of 116. I chose this value because usually larger numbers tend to intimidate people, including myself but the steps in evaluating this square root are actually quite simple.
Step 1- I recognized that  is not a perfect square, as 116 cannot be expressed as the product of two equal integers.
is not a perfect square, as 116 cannot be expressed as the product of two equal integers.
Step 2- I know that in order to estimate the value of  I need to find the two perfect squares that it falls between, which as we know are 100 (
I need to find the two perfect squares that it falls between, which as we know are 100 ( 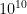 ) and 121(
) and 121(  ).
).
Step 3- Calculate the difference between 116 and 100 and 121 and 116. You will find that 116 is closer to 121. We now need to evaluate  = 10 and
= 10 and 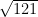 = 11. This means my value must fall between 10 and 11 but is closer to 11.
= 11. This means my value must fall between 10 and 11 but is closer to 11.
Step 4- I estimated my value to the nearest 10th and because the value is closer to 11, but cannot surpass it, my educated estimate is  ≈ 10.8
≈ 10.8
Example 3.

Further explinations of example 3.
Step 1- Recognize that ![\sqrt[4]{79} \sqrt[4]{79}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B79%7D&bg=ffffff&fg=000000&s=0) is not a perfect fourth, it is not a number that is equal to being multiplied by itself four times. How do you know this? It takes a bit of memorization if you choose to do so; however, the perfect fourths can be learned by continuing the multlipication of perfect squares and cubes: (i.e.
is not a perfect fourth, it is not a number that is equal to being multiplied by itself four times. How do you know this? It takes a bit of memorization if you choose to do so; however, the perfect fourths can be learned by continuing the multlipication of perfect squares and cubes: (i.e. 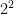 = 4 which is the perfect square, multiply 2 to the power of 3 for the perfect cube:
= 4 which is the perfect square, multiply 2 to the power of 3 for the perfect cube:  = 8 and
= 8 and  = 16 which is the perfect fourth.
= 16 which is the perfect fourth.
Step 2- After listing out the first few perfect fourths, I saw that 79 must fall in between ![\sqrt[4]{16} \sqrt[4]{16}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B16%7D&bg=ffffff&fg=000000&s=0) and
and ![\sqrt[4]{81} \sqrt[4]{81}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B81%7D&bg=ffffff&fg=000000&s=0) . After finding our two perfect fourths, we must evaluate
. After finding our two perfect fourths, we must evaluate ![\sqrt[4]{16} \sqrt[4]{16}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B16%7D&bg=ffffff&fg=000000&s=0) = 2 and
= 2 and ![\sqrt[4]{81} \sqrt[4]{81}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B81%7D&bg=ffffff&fg=000000&s=0) = 3.
= 3.
Step 3- I calculated the difference between 79 and 16 and 81 and 79; 79-16 = 63 and 81-79 = 2. We have now indicated that ![\sqrt[4]{79} \sqrt[4]{79}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B79%7D&bg=ffffff&fg=000000&s=0) is significantly closer to the value of 3, but cannot surpass it.
is significantly closer to the value of 3, but cannot surpass it.
Step 4- Educated estimate! ![\sqrt[4]{79} \sqrt[4]{79}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B79%7D&bg=ffffff&fg=000000&s=0) ≈ 2.9
≈ 2.9
Glossary
Perfect cube: a number that is multiplied by itself three times
Perfect fourth: a number that is multiplied by itself four times
Perfect square: the product of a rational number multiplied by itself
Power: (aka an exponent) is a number that states how many times you need to multiply the number by itself
Radical: The √ symbol that is used to denote square root or nth roots, it consists of the root symbol, the radicand (number within the root symbol) and when dealing with anything greater than perfect squares, an index which is a small number on the left of the square root tells us how many times a term has been multiplied by itself.
Square root: a number which produces a specified quantity when multiplied by itself











 On September 15, 1835 on the return route across the Pacific, the Beagle arrived in the Galapagos Islands where Darwin would make his most notable discoveries. It was here on the Galapagos, that Darwin discovered the vast diversity of different animals on the islands, some species being exclusively located on the Galapagos, such as the finches he discovered.
On September 15, 1835 on the return route across the Pacific, the Beagle arrived in the Galapagos Islands where Darwin would make his most notable discoveries. It was here on the Galapagos, that Darwin discovered the vast diversity of different animals on the islands, some species being exclusively located on the Galapagos, such as the finches he discovered. He noticed that
He noticed that 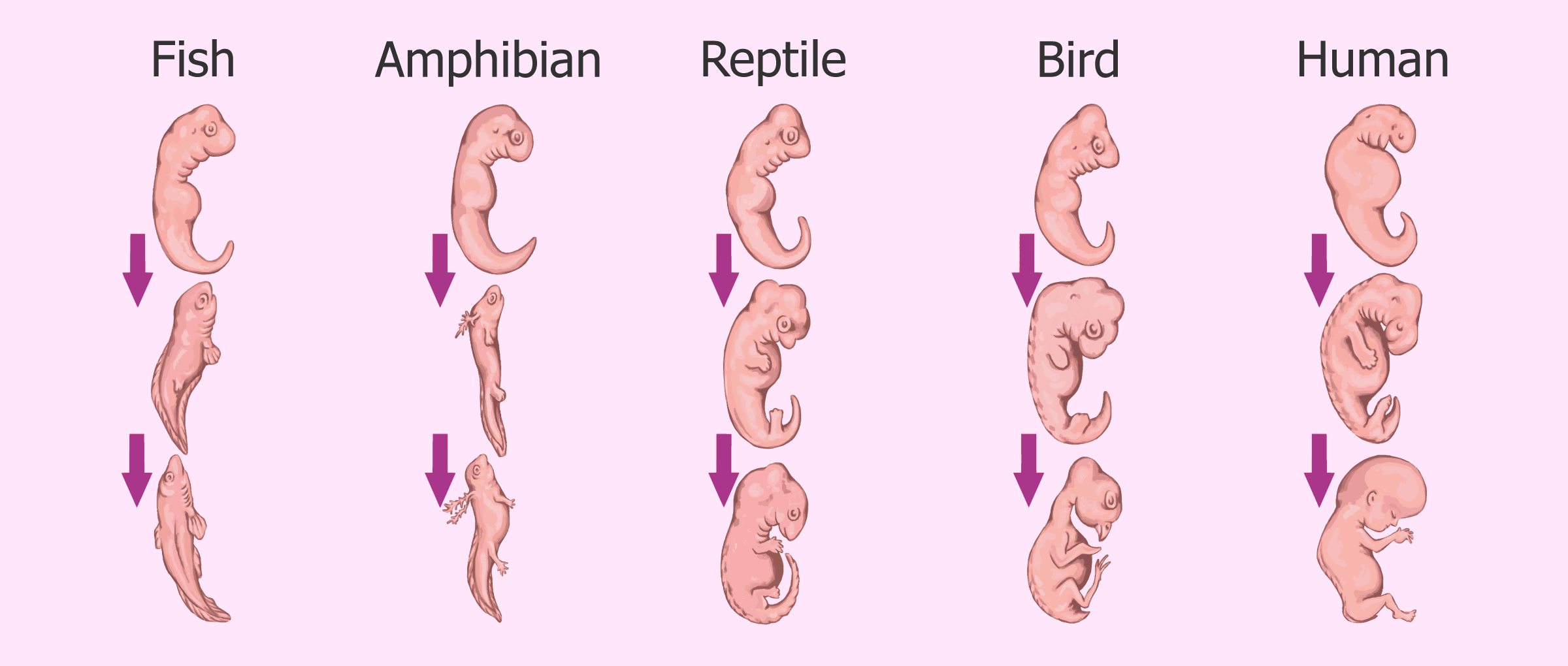 (biologyonline). For example, all vertebrate embryos have gill slits and a tail during early stages of development. The developmental patterns of these species begin to differ as development advances, which explains why the embryonic tail of a human is now a tailbone, and the ‘gill slits’ develop to become into the jaw and inner ear. These shared features suggest that all living things descend from a shared ancestor, and that this ancestor had DNA as its genetic material, used the genetic code, and expressed its genes. The reason that we do not still have our tail, and why we differ from birds or fish is due to Mutation. Hox genes encode transcription factors and are necessary during embryonic development for determining how the cells in a specific region develop, however all that is needed to determine if an animal has arms, or gill slits is a few mutations. This process entails a piece of DNA called a ‘switch’ that turns “on” or “off” genes. (What Darwin Never Knew). Genes are turned on and off in different patterns during development to allow for the differentiation of cells. This connects back to Darwin’s theory of evolution because it the reason that all species of life are related but evolve to become different. A great example of how mutations coded for a new species is that of many prehistoric fish, specifically that of the Tiktaakik.
(biologyonline). For example, all vertebrate embryos have gill slits and a tail during early stages of development. The developmental patterns of these species begin to differ as development advances, which explains why the embryonic tail of a human is now a tailbone, and the ‘gill slits’ develop to become into the jaw and inner ear. These shared features suggest that all living things descend from a shared ancestor, and that this ancestor had DNA as its genetic material, used the genetic code, and expressed its genes. The reason that we do not still have our tail, and why we differ from birds or fish is due to Mutation. Hox genes encode transcription factors and are necessary during embryonic development for determining how the cells in a specific region develop, however all that is needed to determine if an animal has arms, or gill slits is a few mutations. This process entails a piece of DNA called a ‘switch’ that turns “on” or “off” genes. (What Darwin Never Knew). Genes are turned on and off in different patterns during development to allow for the differentiation of cells. This connects back to Darwin’s theory of evolution because it the reason that all species of life are related but evolve to become different. A great example of how mutations coded for a new species is that of many prehistoric fish, specifically that of the Tiktaakik. (What Darwin Never Knew). It has the body of a fish with scales, but also the bone structure is seen in all four-legged forms. The fish evolved into what we know as modern-day land animals. However, some of the same bone structure remains between fish and land animals such as human. Another example is the biological composition of human and chimps. Chimps are human’s most closely related relative, with only a 1% difference in DNA. (What Darwin Never Knew) Once again, mutation is responsible for the evolution into different species. After the separation of ancestor lineages, human and chimpanzee genomes experienced various mutations such as single nucleotide substitutions, deletions, and duplications of DNA fragments of different size, insertion of transposable elements and the rearrangements of chromosomes. (Live Science). Differences in the sequences of DNA that turn genes on and off, and through sequences of the DNA that throw switches, is what is responsible for the large changes of different organisms, despite only small differences in the DNA molecule itself. This shows how small differences in DNA can generate enormous change.
(What Darwin Never Knew). It has the body of a fish with scales, but also the bone structure is seen in all four-legged forms. The fish evolved into what we know as modern-day land animals. However, some of the same bone structure remains between fish and land animals such as human. Another example is the biological composition of human and chimps. Chimps are human’s most closely related relative, with only a 1% difference in DNA. (What Darwin Never Knew) Once again, mutation is responsible for the evolution into different species. After the separation of ancestor lineages, human and chimpanzee genomes experienced various mutations such as single nucleotide substitutions, deletions, and duplications of DNA fragments of different size, insertion of transposable elements and the rearrangements of chromosomes. (Live Science). Differences in the sequences of DNA that turn genes on and off, and through sequences of the DNA that throw switches, is what is responsible for the large changes of different organisms, despite only small differences in the DNA molecule itself. This shows how small differences in DNA can generate enormous change. 









