Mistake of the week-17
Math Vocabulary:
Quadrants– The four sections that are created when there is an x and y axes plane.
Standard Position (Initial arm)– The initial arm is where we start from, in this case our initial arm will always be the x-axis between quadrant 1 and quadrant 4.
https://www.expii.com/t/standard-position-of-an-angle-5217
Terminal arm (terminal side)- Where we end, it can be in any quadrant.
Rotation Angle– Amount of rotation (angle) between the initial arm and terminal arm.
Reference Angle– The reference angle can be in all four quadrants, it is the angle formed by the terminal side, always from the horizontal (x-axis). Always less or equal to 90°.
Ratios– Ratios used to find missing sides or angles of a triangle. The three ratios are sine, cosine, and tangent.
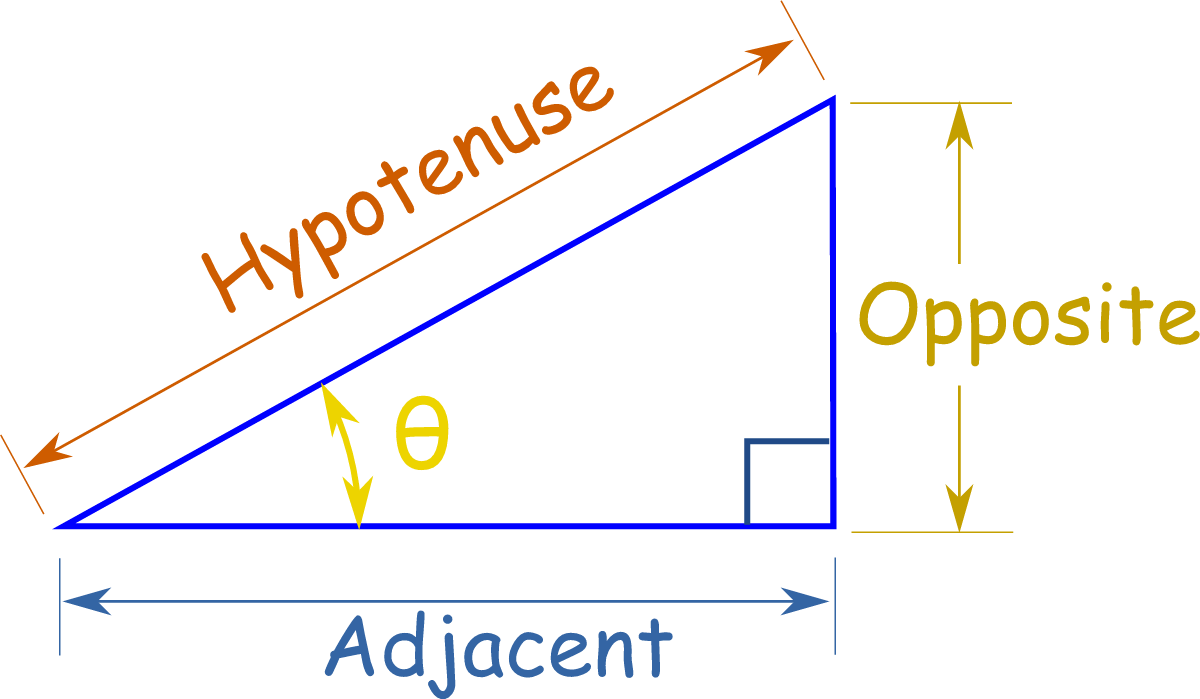
Hypotenuse- Longest side of the triangle, always across the 90°.
Adjacent- This depends on where the reference angle is located, but it is always in the side that is right besides it.
Opposite- This depends on where the reference angle is located but it is always opposite to it.
https://www.mathsisfun.com/algebra/trig-finding-side-right-triangle.html
Special Right Triangles- These are triangles that are very common and their ratios are always the same. When we encounter one of these triangles, a calculator is not needed because the values never change.
Ambiguous Case- Triangles can be located in different quadrants, however, it is really difficult to determine this unless we draw and solve the triangle. Ambiguous means that is really difficult.
Sine Law- This is a very common law used when you do not have a right triangle.
Cosine Law– This is used when you do not have enough information to use the Sine Law.
Best mistake of the week:
Practice sheet, Law of Sines Ambiguous Case, number 3:
My mistake:
It is not really a mistake but I did not understand why it was giving me an error when I first tried to solve it.
Why is this important?
It is important to know what the reasons for the calculator giving you an error might be. It might be because the formula was written incorrectly or like in this case, the problem had no solution at all. To prevent this it is important to remember the basic rules of the problem you are solving.
What I did:
Here is how I drew the triangle and plugged the formula into my calculator.
Solution:
This is why the formula I was using never worked.
There are zero triangles, this triangle is not real nor possible.
The solution is correct.