When you are working with polynomials and want to check your answers there are some methods you can use.

The easiest way to check your answers is by replacing the variable (s) with a number.

It is recommended to use a number between 2-10, the commonly used numbers are 3, 4, and 5.

To use this method, you first have to expand and simplify the polynomial.

First example:

After having the expanded answer you will be able to check if it is correct, to do this you first need to rewrite the expanded answer but replacing the variable with any number. Do the same process but with the original polynomial (you have to use the same number used before as the variable):

If the answer is the same in both sides, it means that the simplified answer is right.

Second example:

This method will make your checking process much easier and trustful.

Vocabulary—————————————————————————————————————

Expand: Removing the brackets in a equation or expression and simplifying it.

Simplify: To make simple or to reduce a equation or expression.

Polynomial: An expression with constants, variables, and exponents. Poly= Many , Nomial= Terms

Variable: An unknown quantity, usually a number, that can be changed.

• A polynomial is an algebraic expression that can be made up of variables, constants and exponents.

There are three ways you can multiply polynomials, these are:

Algebra tiles version, Area model version, and Distributive law version.

Algebra tiles version:

Used when there is an easy expression that can be represented as tiles:

There are three types of tiles, negative or positive, that represent different degrees:

Basically you have to create a rectangle which in the inside willl have the answer.

Step one: Represent the expression terms horizontally or vertically but each set of terms diagonally of each other.

Step two: Draw long lines in each tile separation.

See example below:

Example:

Remember to use this way of multiplication when it is an easy expression.

The second method is used when there are larger or more dificult expressionss that cannot be represented in algebra tiles but you still have to represent it by drawing:

Area model version:

This method is used by students that are more comfortable representing the expressions as drawings.

The whole expression is written arround a square or rectangle *depending of how many terms are being multiplied*.

Step one: Identify which terms of the expression you will put in the vertical side of the rectangle or square.

Step two: Multiply each vertical term by each horizontal term

See example bellow:

Example:

This method is very usefull if you are a visual learner.

The last method is one of the most used because it does not uses drawings to represent the expression:

Distributive law version:

It is the most used method and you probably have seen it in your workbook.

You have to multiply everything inside the brackets by everything outside the brackets>

Step 1: Expand the expression to make it clearer.

Step 2: Multiply the terms together.

See example below:

*When multiplying like terms with variables, you add the exponents together*

Example:

This is a very useful method when there is no time for drawing or when you simply do not like to draw at all.

*To be able to understand the procedures in this document you have to at least know how trigonometric ratios work.*

Solving a triangle means finding all the parts that are missing and find their values.

To solve a triangle it is necessary to identify which parts are missing, the parts that could be missing are the sides or the angles.

After identifying such parts, you have to find the right method to solve it:

The most common methods are:

Trigonometric Ratios (SOH, CAH, TOA) = Recomended when you have just one value and an inconite.

Pythagorean Theorem ()= Can only be used when you have the value of two sides of the triangle.

Δ 180° (The sum of the inside angles of a triangle will always be 180°) = Used when trying to find angles and when you have at least two known angles.

After doing all of this, you have to pick what you are going to solve first and which method you will use.

Example:

Second Example:

These methods are very useful when you have to find missing angles or sides.

How to find the missing side of a right triangle:

To find the missing side of a right triangle, there are two methods.

The first method and the one I will review today is using trigonometry:

The first step to find the missing side of a right triangle is labeling the sides of the triangle, you have to label the hypotenuse, the opposite side, and the adjacent side. You have to localize the reference angle to be able to label it.

*Remember, the hypotenuse is the largest side of the triangle and it is always across the 90 degrees angle. The adjacent side is directly besides the reference angle, and the opposite side is across the reference angle*

The next step is determining which trigonometric radio, you can use:

Sine, Cosine, or Tangent are the trigonometric radios we will be using.

*A tip to remember the formulas of the different radios is using an acronym, SOH CAH TOA, with this you will remember that Sine is Opposite over Hypotenuse, Cosine is Adjacent over Hypotenuse, and Tangent is Opposite over Adjacent.*

After doing this you have to create an equation using the selected trigonometric ratio.

The formula is:

The last step is to solve the equation.

Procedure:

Examples:

I hope this works for you as well as it does to me,

Thank you for reading.

Scientific notation is a way to express very large or very small numbers in an easier, and compacted form.

Any number can be represented as scientific notation, they are expressed as the product of two factors.

The formula is:

The first factor, “a” can be any number between 1 and 10

The second factor is a power of 10, which means it is 10 to the power of x, x represents a variable. This variable can be negative or positive and depending of it, you can see which side was the decimal point moved.

How to convert large numbers:

If we have a large number, such as 1943000000000, it is difficult to read and work with. However,  if we convert it to scientific notation, it will be much easier.

To do this we have to move the decimal point to the left side, until there is only one digit before the decimal point.

*Remember every number has a decimal point, in positive numbers it is not written but it is at the end.*

1943000000000

We moved the point 12 times to the left, this means that we divided by 10 twelve times. Our second factor will be 10 to the power of 12 ().

We also have our first factor, when we moved the decimal point 12 times, the number 1.943 was left, the zeros disappear so we keep the natural numbers.

Our final answer will be:

Check:

*To check the answer. you have to do the multiplication and if it is right you should get the same number that you started with.*

Examples:

• 12000

We moved the decimal point 4 times, so it is

Final answer:

• 17840000000000

We moved the decimal point 13 times, so the second factor is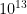

Final answer:

How to convert very smalls numbers into scientific notation:

Now to convert very small numbers into scientific notation, there are three things that change.

• Instead of moving the decimal point to the left, you are moving it to the right.
• The exponent of the base 10 power will not longer be positive, instead it will be written as a negative exponent.
• You stop moving the decimal when you get to the first digit that is not 0.

So, when there is a number like 0.0000000246, you have to move the decimal place to the right:

0.0000000246

We stop after the 2 because is the first digit different than zero.

Like before zeros also disappear.

We moved the decimal point 8 times to the right, the factor will now be 10 to the power of negative 8 ().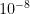

Final answer:

Examples:

• 0.0067

We moved the decimal point 3 times, so it will be

Final answer:

• 0.00000002328

We moved the decimal 8 times, so it will be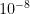

Final answer:

This is how you can convert any number and write it as scientific notation.

VOCABULARY

Exponent/Power: A way to express the number of times a number is multiplied by itself.

Factor: Number we can multiply to get another number as result (product).

Variable: It expresses an unknown number.

How to find the great common factor (GCF) and the least common multiple (LCM) using prime factorization?

Using prime factorization to find the GCF and the LCM is very useful, you can find the GCF and the LCM of large numbers in a small amount of time in just 4 steps.

• The steps to find the GCF and the LCM are simple:

Step 1: Find the number’s factor.

Step 2: Write down all the factors and pair them up.

After doing this you can find the GCF and the LCM:

• To find the GCF , there is only one step you should follow:

Step 1: Multiply the numbers that have a pair with each other, for example: if 2 and 5 have a pair you should multiply (Attention, you shoud not multiply ,  because you just have one digit per pair.).

• To find the LCM, there is also only one step after finding the GCF:

Step 1: Multiply the GCF with all the numbers that does not have a pair.

Examples:

10 and 25

8204 and 504