Math 11 – Adam’s Blog

Top 5 things I learned in Pre Calculus 11

Adam on January 21, 2022

This year in Pre Calculus 11 I learned a lot.

#1 Perfect Squares

Perfect Squares have helped me a lot this year in Pre-Calculus 11, it was one of the first things that we learned in the course. I ended up memorizing the perfect squares from 1-15. Memorizing these set of numbers just generally helped me with certain types of equations, especially with our first and second unit which were Roots and Powers, and Radical and Radical Operations. Having a list of perfect squares in your head will be very helpful through all semi advanced levels of math without being able to use a calculator.

Square 1 to 30 | Values of Squares from 1 to 30 [PDF Download]

#2 Radicals

Radicals in math are very important. By using radicals as inverse operations to exponents, you can solve almost any exponential equation. Radicals are also another key building block to solving exponential equations, and helped me a lot during our first 3 units which were; Roots and Powers, Radical and Radical Operations, and Solving Quadratic Equations.

Section 4.3 Mixed & Entire Radicals. - ppt download

How to Teach Simplifying Radicals ⋆ Algebra 1 Coach | Teaching math, Teaching algebra, Simplifying radicals

Radicals Maths | Simplifying Radicals, Equations and Functions

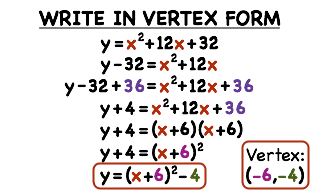
#3 Completing the Square

Completing the square put simply just made the course easier. Learning this in unit 3 helped a lot with our next unit Analyzing Quadratic functions. It can be challenging to learn at the start, but it is worth putting in the work to learn this skill. It mainly helped with Quadratic equations, being easier than the Quadratic formula but a lot harder than just factoring.

How Do You Convert a Quadratic from Standard Form to Vertex Form by Completing the Square? | Printable Summary | Virtual Nerd

#4 Adding and Subtracting Radical Expressions

Adding and Subtracting Radical Expressions is also another building block for other skills or concepts. In future courses, knowing how to add and subtract radicals will come in very handy as well as it helped solve any exponential equation that I have faced this course.

#5 The Cosine Law

The Cosine Law is one of the two laws that we learned this year in Pre-Calculus 11. The other law that we learned was called the Sine Law. The Cosine law is an important skill because of it’s use in real life. I had never heard of The Cosine Law before this unit, so it was interesting to learn about it.

Week 16 Pre Calc 11

Adam on January 17, 2022

This week in Pre Calc 11, we finished our trigonometry unit. We did the Sine Law and the Cosine Law.

The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known. It can also be used when two sides and one of the non-enclosed angles are known.

The Sine Law has two formulas

This is the formula for finding an angle:

$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}$

This is the formula for finding a side:

The law of cosines is useful for computing the third side of a triangle when two sides and their enclosed angle are known, and in computing the angles of a triangle if all three sides are known.

The Cosine Law has two formulas

This is the formula for finding an angle:

This is the formula for finding a side

In Triangle KMN, KM = 25.0 m, MN= 24.6 m, and Angle K = 75 degrees

First we need to check to see if it is an ambiguous case. We can do this by checking to see if the measurement length directly across the angle given is the shortest. In this case, it is so there is possibly another triangle.

Let’s try an example for Cosine,

Pre Calculus 11 Core Competency Reflection

Adam on January 14, 2022

Download

Week 15 Pre Calc 11

Adam on January 5, 2022

This week in Pre Calc 11, we started our trigonometry unit. One thing I really took out from it would be Angles in Standard Position in All Quadrants.

For example, a question could be:

The point P(2, -5) lies on the terminal arm of an angle θ in standard position.

a) Determine the primary trigonometric ratios of θ.

b) Determine the measure of θ to the nearest degree.

So for a, we need to determine r, because we already have the x and y points.

Determine the angles between 90 and 360 degrees that have the same reference angle.

Week 14 Pre Calc 11

Adam on December 13, 2021

This week in Pre Calc 11, we learned more about applications of rational expressions, had our unit test, and started reviewing grade 10 Trigonometry. Today I will explain how to do one type of the word problems we had to face this week.

Bronwyn rides her electric bicycle 10km/h faster than Aaron. Bronwyn can travel 60 km in the same time that it takes Aaron to travel 40 km. Determine Bronwyn’s average speed and Aaron’s average speed.

First of all, let Aaron’s speed be x and Bronwyn’s speed be x+10. The other information that we can take from this is the distance. Bronwyn’s being 60 km and Aaron’s being 40 km. These are equal to each other.

To make an equation from this, we can use x and x+10 as the denominators. So, it will look like this:

$\frac{}{x+10}$ = $\frac{}{x}$

They are equal to each other because they travel the distances in the same time.

Now, for the numerators, we can put the distances ie: 60 and 40 in there.

So it should look like this:

$\frac{60}{x+10}$ = $\frac{40}{x}$

From here, it is just solving. Since there are only two fractions, we can cross multiply them. This comes out to

60x= 40x +400

Now we just -40x to get

20x= 400

Divide both sides by 20

x=20

Aaron’s average speed is 20 km/h. Bronwyn’s average speed is 30 km/h.

Let’s try another example,

A boat travels 4 km upstream in the same time that it takes the boat to travel 10 km downstream. The average speed of the current is 3 km/h. What is the average speed of the boat in still water?

Let the average speed of the boat in still water be x km per hour. So then the average speed downstream would be (x+3), and the average speed upstream would be (x-3). The distance downstream is 10 km

So, the time downstream is $\frac{10}{x+3}$

The average speed upstream is (x-3), and the distance upstream is 4 km.

So, the time upstream is $\frac{4}{x-3}$

It takes the same time to travel upstream as it does to travel downstream.

So, an equation is: $\frac{10}{x+3}$ = $\frac{4}{x-3}$

We can cross multiply this equation again. This comes out to

10x – 30 = 4x + 12

Now we can move the 4x to the other side and change the sign

6x – 30 = 12

Move the -30 to the other side and change the sign

6x = 42

Divide both sides by 6

x = 7

So, the average speed of the boat in still water is 7km/h.

Week 13 Pre Calc 11

Adam on December 5, 2021

This week in Pre Calc 11, I learned how to add and subtract Rational Expressions. This week we mainly focused on adding and subtracting rational expressions and a bit of equations. In this, I will be talking about adding and subtracting rational expressions, as well as solving rational expressions.

First, you have to make a common denominator, then simplify from there.

Let’s try a simple question:

$\frac{5}{3x^2}$ + $\frac{x}{2}$

So in this question, we need to find a common denominator. The common denominator for this question would be $6x^2$ . So we need to multiply $\frac{5}{3x^2}$ by 2, and we need to multiply $\frac{x}{2}$ by $3x^2$ . This will equal $\frac{10}{6x^2}$ + $\frac{3x^3}{6x^2}$ . From here we can get rid of the fraction and just have $10 + 3x^3$ . Now all we have to do in this question is simplify, so we do not have to go any further.

Now, let’s try a harder question:

$\frac{2x}{x+3}$ + $\frac{3x}{2x + 8}$ ÷ $\frac{x^2}{3x +12}$

$\frac{2x}{x+3}$ + $\frac{3x}{2(x + 4)}$ x $\frac{3(x+4)}{x^2}$

So, we can cancel out the x+4 and we can cancel the x out too. So this comes out $\frac{2x}{x+3}$ + $\frac{3}{2}$ multiplied by $\frac{3}{x}$

From here we can use bedmas and simplify this equation we can multiply and this comes out to $\frac{2x}{x+3}$ + $\frac{9}{2x}$

At this point we need to find a common denominator to further simplify this. The common denominator that we will use is 2x(x+3). So we need to multiply 2x by 2x, and we need to multiply 9 by (x+3). This comes out to $\frac{4x^2 + 9x +27}{2x (x+3)}$ . This is the final solution to this question.

Here’s another example: $\frac{2d}{d^2 - 6d +8}$ + $\frac{3}{d^2 - d -2}$

First we can factor both the bottom denominators

This is what it comes out to:

$\frac{2d}{(d-2)(d-4)}$ + $\frac{3}{(d+1)(d-2)}$

Now we need to find a common denominator. The common denominator will be (d-2)(d-4)(d+1)

So we need to multiply the first fraction by (d+1), and the second fraction by (d-4)

This comes out to $\frac{2d^2 +2d +3d -12}{(d-2)(d-4)(d+1)}$

This simplified would be $\frac{2d^2 +5d - 12}{(d-2)(d-4)(d+1)}$

Now, we need to simply the top. To do this, we need to factor it. This comes to our answer which is:

$\frac{(2d -3)(d+4)}{(d-2)(d-4)(d+1)}$

Week 12 Pre Calc 11

Adam on November 28, 2021

This week in pre calc 11, we learned about how to solve rational expressions, which specifically are fractions with variables. This week we mainly focused on multiplying and dividing rational expressions, which is what I will cover here. Another very important thing we learned is non-permissible values that x or any variable cannot be in that equation.

Here is a few examples of what rational expressions would look like:

$\frac{4x}{x+2}$ $\frac{3}{x-2}$ $\frac{x}{x^2-6x+8}$ $\frac{3}{(x-1)(x-2)}$

These expressions cannot contain square roots or variable exponents.

A limitation, the domain, or values that the expression cannot be specified by are all examples of non-permissible values. This indicates that some integers, when substituted for x, result in a denominator of zero. The equation can still be simplified when the numerator is zero. This is not feasible when the bottom of the fraction (the denominator) is 0. As a result, these are prohibited. Use the equal sign with a line across it to indicate these constraints, which means “x cannot equal…”

These are the non-permissible values for the expressions above:

x≠-2 x≠2 x≠ 2, 4 x≠ 1,2

Here is an example of an equation, then to be simplified to non-permissible values:

$\frac{x}{x^2-6x+8}$

$\frac{x}{(x-2)(x-4)}$

So, the non-permissible values would be 2 and 4, in other words x≠ 2,4

Let’s try a harder example:

$\frac{x^2 - 9}{x^2+8x +15}$

We can factor both the top and bottom and simplify from there.

$\frac{(x-3)(x+3)}{(x+3)(x+5)}$

From here our non permissible values are: -3, -5. So x≠ -3, -5

Week 11 Pre Calc 11

Adam on November 21, 2021

This week in Pre Calc 11, I learned how to solve word problems using quadratic equations and the vertex.

Let’s try an example,

Two numbers have a difference of 6 and their product is a minimum. Determine the numbers.

So first of all, we need to create an equation and set the two numbers values. So, we can set the first number to equal x, and we can have the second number equal x-6. To make an equation out of this it can be x(x-6). The first thing we are going to do is distribute which we get $x^2-6x$ . From here, we can pretend the third number is equal to 0, from this we get $x^2-6x+0$ . Next, we need to complete the square. The first step of completing the square is dividing the second term by 2, and squaring it. This comes out to $(x^2-6x+9-9)$ . Next we get $(x^2-6x+9) -9$ . From here we have to factor the 3 terms, which gets $(x-3)^2 -9$ . From this equation we get the vertex, which is (3,-9). We get our first number of the two numbers, which is 3. We can put the 3 back into our original equation and get the second number of the two. So, this would be 3-6, which is just equal to -3. Which is our second number.

Let’s try another harder example,

A rectangular play area is to be bounded by 120 m of fencing. Determine the maximum area and the dimensions of this rectangle.

In this question, we are trying to find the area, which is just length times width. We need to find an equation to do this. I have $120 - 2w$ and this is all divided by 2. So, we know by this that the length is 60 – w. We now have an equation to solve this. Again, we make the first number w, and the second one 60 – w. So our equation is w(60 – w), and this comes out to $60w - w^2$ . To rearrange this it would look like $-w^2+60w$ . So next, we want to make the $w^2$ positive, so we can divide all of the terms by -1. This comes out to $-(w^2 - 60w)$ . From here, we need to complete the square. Which comes out to $- (w^2 -60w + 900- 900)$ . From here we need to take the -900 out of the bracket and the – sign will affect this and make it positive. This is what it will look like $- (w^2 -60w + 900) +900$ . Next, we need to factor the 3 terms. This comes out to $- (w -30)^2 +900$ . This now gives us our vertex. The vertex is 30, 900. We can put the 30 back into our original equation to get our length. So we have 120 – 2(30) all divided by 2. Which will equal 30.