Week 6 – Solving Quadratic Equations

Posted on by shannonf2015

This week, we have learned how to solve quadratic equations by completing the square and applying the quadratic formula when the equation is not factorable.

A quadratic equation includes at least one squared variable and has the following form: ax² + bx + c = 0

a, b and c are constants or numerical coefficients and x is the unknown variable.

Let’s start with the method of completing the squares. This method is quite a long process, it depends on the equation. The best would be to see if it is factorable, if it is not or factoring is too difficult for the equation, you can use the completing the squares method or using the quadratic formula.

Completing the Squares 

Lets start with an example:

{x^2}+{4x}=2

To be able to solve this equation, it must equal to zero as it is a quadratic equation. In this example, we have to move the 2 to the other side so that it becomes zero:

{x^2}+{4x}-2=0

It becomes -2 because when you move it to the other side of the equation, you switch the signs.

Now that we have it written in the proper equation for us to solve, first check if it is factorable. As there are no numbers that both multiply to equal to two and add to equal 4 (only option is 2\times{1}). So we must use either the completing the squares or formula. In this example, I will be using the completing the squares method.

First, we make two places that are both + and – to get zero pairs in between the inner term and the constant:

 

Then we find what is the missing constant. To do that, we divide the inner term in two and square it. The answer will be 4. Then we factor for those three terms.

 

Now that you got {(x + 2)}^2, write the other numbers that are next to it: -4 -2 which equals to -6.

Isolate the variable by moving -6 to the other side of the equation. Then square both sides to get x + 2 = \sqrt{6}. Make sure to include both + and – signs next to the radical because it has two options. 

Then move the 2 to the other side of the equation to isolate x.

x = -2 ±\sqrt{6}

 

Now let’s see how we can apply the quadratic formula. 

{2x}^2-2x-1=0

This is the same form as:

{ax}^2+bx+c=0

a=2, b=-2, c=-1

Formula:

Image result for quadratic formula

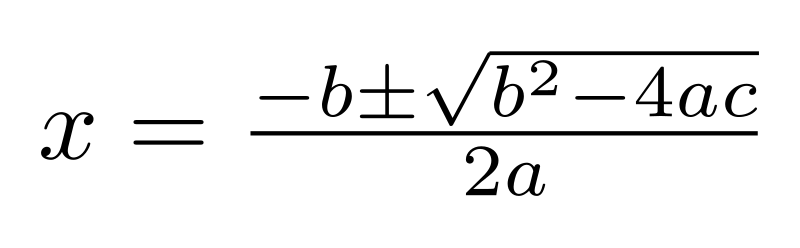
Substitute the variables with the numbers given.

 

Once you substitute it, simplify it while making sure to keep the + and – sign next to the radical.

 

 

Leave a Reply

Your email address will not be published. Required fields are marked *