This week in precalc 11, we learned many new things. We started our new unit, Rational Expressions and Equations. We learned how to multiply, divide, add and subtract rational expressions. What we recalled starting the unit was that a rational number is a quotient of 2 integers and we must know that our denominator can NOT = 0. Therefore the quotient of two polynomials is called a rational expression
What we also learned were non permissible values, the value of a variable that can not be used. Lets say for example we have this :
Since we can not have a 0 as a denominator, we must find the zero’s by factoring the denominator. So we factor which gives us
. This means that x can not = -2 or 1, those are the non permissible values.
The main thing I liked this week and learned was multiplying and diving because it was fairly simple and straight forward. It was simple because while dividing, you just use the reciprocal and then you multiply and for multiplying it is just finding common factors and cancelling out. For example, we have this …
First thing you have to do is factor anything out that you possibly can …
Once everything is factored out, whatever are the same from the top and bottom can be cancelled out (because it would = 1, same number divided by the same thing is = 1)
You are now left with , that is your final answer. We also know that the non permissible values are -4 and -1.
This is a fairly simple example but its just to show how everything works. Factoring plays a big role in solving these types of questions because if you do not factor right, you will not get the right answer. Making sure everything is factored correctly is the key to getting the answer right.
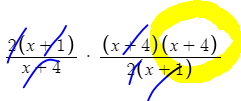
Leave a Reply