This week in precalc 11, we learned a lot of new things. One of my favorite things I learned this week was analyzing y = a(x - p)^2 + q which is standard form

We know that a can tell us …

  • If it is congruent to y = x^2
  • If it is a stretch |a| > 1
  • If it is a compression |a| < 1
  • If it opens up or down

We know that (x - p)^2 can tell us …

  • The horizontal translation
  • If the vertex is moving to the left or the right

We know that q can tell us …

  • The vertical translation
  • If it is moving up or down

When we first started this unit, I was very confused with the equation and what each part meant but when we finally learned this, it helped me understand the graph very well.

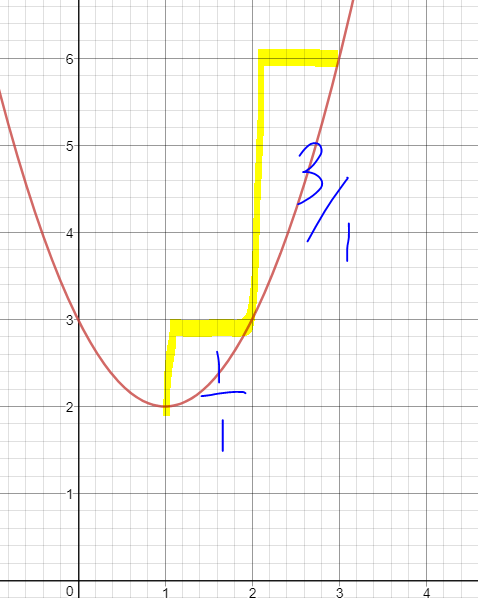
Ex : y = (x - 1)^2 + 2

  • Since we know that the a is positive and = 1, we know its congruent to the parent function (1, 3, 5)
  • The trick I’ve learned is that with the (x - 1)^2, if the inside of the brackets is negative, it’ll be going to the right (positive). But if the insides brackets is positive, it’ll be going to the left (negative). So in this case we know that the horizontal translation will be one to the right.
  • With the 2, since it is a positive it means the vertical translation will be two spaces upwards.
  • With the information we have, if from (0,0) we have a horizontal translation (x) of one space to the right, and a vertical translation (y) of two spaces up. Our vertex is (1,2) (opens up and is a minimum vertex)

With all this information, it will be super easy to graph this for me. It is very useful and only takes me 30 seconds to figure everything out.

As you can see in the graph, the vertex is (1,2) and since we know its congruent to the parent function, you go in the pattern (1, 3, 5) as shown.