I am not a math person. I do not have a brain made to solve equations, and I have never liked numbers too much. Instead, I am more of a letter-and-word person. I love stories, and I like writing them even more.
Math has never really told me much of a story, until I started Algebra. To solve an algebraic equation, you need to tell a story or you’re going to get a big fat zero on that test you spend a week worrying about. Those little math equations with letters actually made sense for me – finally! Something that clicked! When I started this unit in my grade seven math class, I finally decided maybe, just maybe, I could like math.
Prior to this epiphany, if anybody asked me what my most hated subject was, I would automatically say Math. The numbers confused me and swam around my brain, meaningless and pounding my skull. I could bluff my way through textbooks well enough, I just never figured out why. I didn’t like math because I am a “Why” person, like one of those kids that constantly asks “why” after an answer is given until their victim becomes infuriated. Until I started delving deeper into math equations, I only wanted to know why these equations existed and why I had to do them in a specific way.
I hated math with a passion by the beginning of middle school, but not only because I wasn’t getting any valid answers – I didn’t understand it. Normally, everything I learn in school clicks in my head. It makes sense, and I can easily explain it to someone. But I never had that in math, especially long division. All the different equations I had to do and numbers I had to keep track of simply hurt my head and made me want to burn the worksheet. That is when my grades began to suffer, but soon enough, a teacher explained it to me in a way that finally made sense – with words. He explained the equations with stories and told me that’s how I learned. Since then, I have remembered this. When I struggled with integers, I made a story for each equation involving a man named Bob walking back and forwards.
Math was never a very significant part of my growing up, besides something to despise. But stories always have been, so if a math equation can have a beginning, a middle, and an end, I’ll be okay.
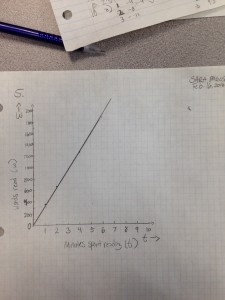
 The Kindle can tell you how many minutes is left in the book you’re reading based on how fast you read. It knows how quickly you turn the page, and can thus assume how many words you can read in a minute.
The Kindle can tell you how many minutes is left in the book you’re reading based on how fast you read. It knows how quickly you turn the page, and can thus assume how many words you can read in a minute.