Archive of ‘Math 11’ category
This week we learned about parabolas and how they can be translated on a graph.
A translation is an image of the original parabola, but moved either horizontally or vertically from the original parent equation 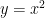

Depending on the equation, you can determine where the parabola has moved on the number line.
If the coefficient of  changes, the parabola will either stretch or compress. A coefficient less than 1 will cause the parabola to compress, while a coefficient more than 1 will cause it to stretch.
changes, the parabola will either stretch or compress. A coefficient less than 1 will cause the parabola to compress, while a coefficient more than 1 will cause it to stretch.

If the coefficient  is negative the parabola will open down, while if it’s positive it will open up.
is negative the parabola will open down, while if it’s positive it will open up.

In the case that your equation looks similar to 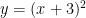 , with your numbers in brackets, then the “c” will effect whether your parabola translates left or right. If the number is positive, it will translate left, and if it’s negative it will translate right. It does not follow the general idea that negatives go left and positives go right.
, with your numbers in brackets, then the “c” will effect whether your parabola translates left or right. If the number is positive, it will translate left, and if it’s negative it will translate right. It does not follow the general idea that negatives go left and positives go right.

While solving quadratic equations, it’s useful to take a look at the discriminant.
The discriminant is area under the square root in the quadratic formula:
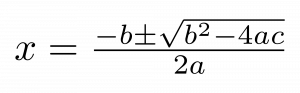
if you have a quadratic equation (equation equal to zero with 3 distinct parts), you can use the quadratic formula to solve. Depending on the answer, we can figure out whether the equation will have 1,2 or 0 solutions.
~
Let’s find the discriminant of the equation: 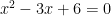
In a quadratic equation, the parent would be 
following the parent, in our equation, a=1, b=-3, and c=6
using this information we can plug in the numbers to our equation to find the discriminant.
If 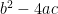 is our equation, we just put our numbers we found in the spots of the letters, and simplify.
is our equation, we just put our numbers we found in the spots of the letters, and simplify.
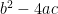


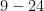
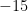
using this we know that since the discriminant is -15, the original quadratic equation does not have any solutions, and using the quadratic formula would not work.
This week we learned how to solve a quadratic equation using factoring.
In order to solve the equation the zero product law must be used.
a*b=0, so either a=0 or b=0.
both sides if the equals sign must be equal.
for example: 8(x+2)(x-7)=0
x+2=0
so x=-2
also, x-7=0
so x=7
a quadratic equation has two possible answers. If you plug either of them into the equation, it should work.
8(x+2)(x-7)=0
x=-2
8(-2+2)(-2-7)=0
8(0)(-9)=0
8(0)=0
0=0
to solve any quadratic equation, the product must be 0. The equation cannot work without it.
When factoring polynomials, we can use a system:
Common?
Difference of squares (2 terms)
Pattern ( x #) (3 terms)
x #) (3 terms)
Easy 
Ugly 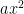
or for an easy jingle, Can Divers Pee Easily Underwater.
using these steps we can factor each type of polynomial to its simplest form.
for example:
3y(y+2) – 9(y+2)
because this polynomial has a common factor, y+2, we can substitute it for an unknown variable such as “a”
3ya – 9a
doesn’t that look better?
now we can use the D to find the difference of squares because there’s 2 terms. If there are more than two terms you can skip the D and go right to P.
3a is common on both terms so we simplify polynomial to
3a(y-3)
now we substitute our y+2 back for “a”.
3(y+2)(y-3)
and you’re done! this polynomial cannot be simplified farther.
For a polynomial with 3 terms, you will not use the D, but skip right to P depending on whether you have  or
or 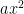 will decide if you use the E or the U.
will decide if you use the E or the U.
When dividing radicals, the denominator can never be a radical. So in order to solve, the denominator must first be made into a rational number.

First, use a difference of squares to rationalize the denominator. But since whatever you do to the bottom you must also do to the top, multiply both the numerator and denominator.

now add like terms to get a more simplified expression.

now you can just simplify the expression as far as you possibly can! It’s okay for the expression to not equal a single number.

The absolute value of a real number is defined as the principle square root of the square of a number.
for instance the absolute value of 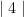 is 4
is 4
when a number is between the brackets, it must be brought out of the bracket like this:
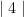

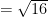
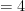
Whenever a number is between brackets, the answer must be a positive number. However, after the number is out of the brackets it can become negative in an equation.
We also learned about roots and radicals. Numbers with square roots can never be negative, like 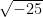 because it cannot be calculated and results in an error when put into a calculator. On the other hand, a cubed number can be negative. Roots with an index that’s even cannot be negative, but roots that have an uneven index can be negative.
because it cannot be calculated and results in an error when put into a calculator. On the other hand, a cubed number can be negative. Roots with an index that’s even cannot be negative, but roots that have an uneven index can be negative.
when simplifying roots that are not perfect, a different approach must be taken.
for example:

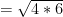 find two multiples of a number, one being a perfect square
find two multiples of a number, one being a perfect square
 separate the roots
separate the roots
 square the perfect square and leave the radical as a square root
square the perfect square and leave the radical as a square root
this applies to other index’s as well, just find perfect cubes instead of perfect squares, etc.
This week we learned about geometric sequences and series. A Geometric sequence differs from an arithmetic sequence because instead of adding a common difference, a common ratio is multiplied by the term to get the next term.
the equation used to find a term in a sequence is
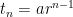
in this equation 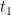 is represented by
is represented by 
for example: 5,10,20,40… find 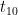
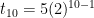

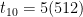
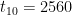
A finite geometric series can be found using the equation

4, 9, 14, 19, 24
 ,
, 
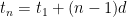
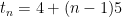

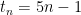
using this information, we can find any value of 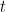 using the equation
using the equation 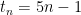 . We can plug in any term into
. We can plug in any term into  to find
to find 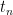
this equation will work for any term within the sequence, as long as the starting term and common difference are constant. If either of these change it is no longer an arithmetic sequence.
To find 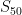 , the sum of all 50 terms, we must use the equation
, the sum of all 50 terms, we must use the equation 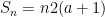
In this equation, 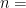 number of terms(50) and
number of terms(50) and 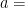 the first term(4)
the first term(4)



changes, the parabola will either stretch or compress. A coefficient less than 1 will cause the parabola to compress, while a coefficient more than 1 will cause it to stretch.
is negative the parabola will open down, while if it’s positive it will open up.
, with your numbers in brackets, then the “c” will effect whether your parabola translates left or right. If the number is positive, it will translate left, and if it’s negative it will translate right. It does not follow the general idea that negatives go left and positives go right.







