Graphing linear inequalities is building off of graphing linear equations. They are graphed the same way, the number before x represents the slope(rise over run) and the second term shows the y-intercept.

The only difference is that when graphed, there is going to be a section shaded. This section represents all the numbers that satisfy the equation. If the line is dotted, those numbers are not included and will be represented by <>. If the line is solid, those numbers will also satisfy the equation and the inequality sign will have an equal on it ≤≥.

To find what the inequality is if the graph is already given.

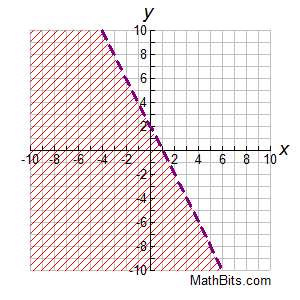
y _ -2x + 2

You create the equation using y = mx + b or slope y-intercept form.

Now, we can take a number in the shaded area and make a true statement.

(0,0) is a coordinate in the shaded area.

0 _ -2(0) +2

0 _ 2

Since 2 is greater than 0 and the line is dotted, we know we need < to make the statement true

0 < 2

We can go back and add < to the blank space of our equation

y  < -2x + 2

 

If we are given the equation to graph, we follow similar steps.

3x + 6 ≤ 2y

Divide by 2 to bring the equation in slope y-intercept form

3⁄2x+3 ≤ y

Once graphed, you can choose any coordinate in one of the sides, (5,0)

3⁄2(5)+3 ≤ 0

15⁄2 + 6⁄2 ≤ 0

21⁄2 ≤ 0

So when graphing, we know to show a solid line because of the inequality symbol and to shade in the side that includes the coordinate that satisfies the equation.

While reviewing, I remembered the importance of restrictions, something that I had to relearn and remember for the coming up midterm.

A restriction makes sure only certain numbers can replace x in a radical so that the radical still works.

For this radical, ∛×, because the radical index is 3 and not a factor of 2, the restriction will always be x∈R x is the element of the real numbers. This is because no matter if the number is positive or negative, it is to the power of 3, it will solve to be positive.

For numbers in square roots and roots with the index like 4, 6, 8, 10, etc, the numbers must be greater than 0 so that they can solve.

√x, x≥0

if there are more numbers under the radical, we solve the inequality.

√(x+5)

x+5 ≥ 0

-5

x ≥ -5

That is how restrictions are found. It is important that restrictions are always shown and matched up with the answers of x to make sure x truly follows its restriction.

 

There are three ways to solve and write the quadratic equation.

General Form

The general form is y =ax² + bx + c

This form tells us the y-intercept, which is c. It tells us the scale, which is a, that is what number changes the 1, 3, 5 scale. This equation does not help us graph it, it tells us it is quadratic by the x², but we can only graph it if it is in factored or standard form.

y =x² + 6x + 9 is an example of a quadratic formula in general form.

Factored Form

Factored form is the first form that is able to be used to solve quadratic equations and graph them. When an equation is formed to factored, it tells you the x-intercepts. It also tells you the scale.

y =x² + 6x + 9 can be factored to y = (x+3)(x+3), which means the only x-intercept is -3, found by taking the factors and solving them to 0 (x+3 = 0, x + -3). This also tells us this is up facing and has the scale 1, 3, 5. Since this quadratic crosses x only once, we can assume it starts there and goes up.

y =x² + 7x + 10 can be factored to y = (x +2)(x+5), so the x-intercepts are -2 and -5 ( x+2 = 0, x+5 =0). This doesn’t help us too much to fully graph because we know where the x-intercepts are, it is up facing, and has the general scale, but we do not know where it starts.

Standard or Vertex Form

This is the most helpful form for graphing, y = (x – p)² + q, (p,q) is the vertex (x,y).

If we have an equation in general form, we can change it to standard form by finding the square.

y =x² + 6x + 8

Find the square means taking the middle term, dividing it by two and then taking it to the power of 2 and then adding that as a 1 (a positive form and negative form). This helps create the factor.

y =x² + 6x + 8

6/2 = 3

3² = 9

A 1 is like 1/1 just like 3/3 is also just 1.

We can then add the 9 back in as a 1, so +9 and -9.

y =x² + 6x +9 -9 + 8

We can then create x² + 6x +9 as a factor (x+3)²

y =(x+3)² -9 + 8

y =(x+3)² -1

We have now a new form that can help us factor. This form tells us the vertex which is (p,q). We also must remember that since the equation has a negative p, the term in its place has been multiplied by a negative. So, when looking for the vertex, it would be (-3, -1). We then find this point of the graph and start from there going up as indicated since there is no negative before the bracket affecting the scale, and going up by 1, 3, 5.

Quadratic Formula

The last way to solve a quadratic equation that cannot be factored is using the quadratic formula. 

y =x² + 3x – 4

First, we list a = 1, b = 3, c = -4

Then it is just filling in the equation.

x = -(3)±√(3)²−4(1)(-4)/2(1)

x = -3±√9+16/2

x = -3±√25/2

x = -3+5/2 0r x = -3-5/2

x = 1 0r x = -4

The parent function of a parabola is y = x²

Vertical translation is shown when there is a term added to x². So, if y = x² + 5, the parent function would be moved 5 units up.

If y = x² – 7, the parent function would be moved down 7 units.

Horizontal translations are shown when y = (x – p)², p being the translation. If the parent function moves 5 to the right, we replace p with 5, y = (x – (5))²

If p = -4, we replace p and the graph moves 4 to the left, y = (x – (-4))² or y = (x +4)²

Now, if we add this together, we can understand how a parent function changes.

y = (x +4)² – 5

This means that the horizontal translation is 4 units to the left, then 5 units down.

The scale can affect whether the parabola is stretched or compressed. If there are no terms before the brackets, the scale is as original, 1, 3, 5, etc. If there is a number higher than 0 in front of the brackets, y = 2(x +4)² – 5, the parabola becomes stretched.

If the number is less than 1 and greater than 0, y = .2(x +4)² – 5, the parabola is compressed.

Lastly, if this term before the brackets is negative, the parabola becomes down facing, y = -(x +4)² – 5

–