20 learning outcomes:
1) Represent repeated multiplication with exponents
Ex: 2 x 2 x 2 x 2 = . The power is how many times the number is multiplied by itself.
2) Describe how powers represent repeated multiplication
Ex: is 3 x 3 x 3 x 3 which equals 81, and
equals 81.
3) Demonstrate the difference between the exponent and the base by building models of a given power, such as and
.
Ex: The base is the number that is multiplied by itself a certain amount of times (the number of the exponent). So and
are different since 2 x 2 x 2 equals 8 while 3 x 3 equals 9.
4) Demonstrate the difference between two given powers in which the exponent and the base are interchanged by using repeated multiplication, such as and
.
Ex: The difference is that both exponents may have the same numbers in them, but they have different sums, since 2 x 2 x 2 equals 8 while 3 x 3 equals 9, they’re the same numbers, but different answers.
5) Evaluate powers with integral bases (excluding base 0) and whole number exponents.
Ex: Any negative base with an even power will always equal a positive since -2 x -2 is 4, but any negative base with an odd power will always equal a negative, for example, -2 x -2 x -2 equals -8.
6) Explain the role of parentheses in powers by evaluating a given set of powers such as ,
and
Ex: The difference is that is (-2)(-2)(-2)(-2) which is 16, while
and
are (-1) x 2 x 2 x 2 x 2 which equals -16.
7) Explain the exponent laws for multiplying and dividing powers with the same base.
Ex: When dividing powers with the same base, you take the first power, and subtract the second power from it. For example, divided by
is just
8) Explain the exponent laws for raising a product and quotient to an exponent.
Ex: When you multiply two exponents with the same base together, you simply add the two powers together, while with division it is the opposite, instead you need to subtract the two powers.
9) Explain the law for powers with an exponent of zero.
Ex: All powers with an exponent of 0 (except 0 as the base) will always equal 1, since for example, equals 4,
equals 1, and
equals 1. As the power goes down by 1, the answer is divided by 2. The answer will always be divided or multiplied by its base depending on if you are adding or subtracting a power.
10) Use patterns to show that a power with an exponent of zero is equal to one.
Ex: As mentioned in question 9, the reason why any power with the exponent of zero will always equal one is due to the fact that as you take away each power, the answer is divided by its base.
11) Explain the law for powers with negative exponents.
Ex: The law for powers with negative exponents states that you need to find the reciprocal of the power, so if you had for example, it would become 1 over
or 1 over 8
12) Use patterns to explain the negative exponent law.
Ex: The reason why you find the reciprocal is because if I were to use 2 as a base for example, is 8,
is 4,
is 2,
is 1 and
is 1 over 2. As you can see from the pattern, as you decrease powers, the answer was divided by 2 each time.
13) I can apply the exponent laws to powers with both integral and variable bases.
Ex: If the number was as an example, it would be -1 x 4 x 4, since the – and the 4 are not in brackets. Is the base was a variable, (a) for example, it would just be the variable and the exponent together, since there isn’t a definite answer until you know what the variable actually equals. So if it was
, it wouldn’t need to be changed at all.
14) I can identify the error in a simplification of an expression involving powers.
Ex: Let’s suppose someone tried to simplify 6
divided by 2
, and they answered with 3
, that is incorrect because if you are dividing powers with exponents, you subtract the exponents from each other (not counting the 6 and 2 base). So the answer is instead 3
.
15) Use the order of operations on expressions with powers.
Ex: If there was a question that asked for I would need to do the brackets first, which would then mean it would simply be
since 5-3 = 2.
16) Determine the sum and difference of two powers.
Ex: The sum of two powers, +
would be 81 + 32 = 113. The difference of two powers,
–
would be 81 – 32 = 49.
17) Identify the error in applying the order of operations in an incorrect solution.
Ex: If the question was 5 x and someone answered with
they would be incorrect since you need to do exponents before multiplication, so it would be 5 x 27 = 135, while
= 3,375, very big difference in answers.
18) Use powers to solve problems (measurement problems)
Ex: Someone has to find the area of a square with the side length of 20cm, a simple way to solve this is to just do which would equal 400.
19) Use powers to solve problems (growth problems)
Ex: A child starts off by getting 2$, they then get double for the next 5 days, how much do they get on the 5th day? An easy way to answer this question is to take the total amount of days, and use that as an exponent, so the answer would be which equals 32.
20) Applying the order of operations on expressions with powers involving negative exponents and variable bases.
Ex: If the exponent or variable base is a negative, you find the reciprocal of it and make the exponent positive. An example is , all that -a is, it just -1 x
, so if you were to answer the question, it would be -1 over
November 9, 2016 at 5:19 am
Awesome stuff, I’m learning lots about exponents. Looking to see more and I will be sure to follow postings on this site.
November 11, 2016 at 9:28 pm
Hi Nicholas, your assignment was well done overall.There are just some errors in some of the questions and explanations that were confusing. You met all of the 20 learning outcomes that you had to describe about but some questions didn’t have explanations (like #2), just examples. Most of your examples were simple but straight to the point which was easy for me to understand. would look like
would look like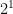 = 1
= 1 . There would be no negative beside the variable.
. There would be no negative beside the variable.
Errors and things forgotten: 3) It asked for a building model of the question
6) Forgot to show what
8) I didn’t really understand when you said add the powers together/divide when you already said multiply the exponents.
9) You said
13) Forgot to show how to apply the exponent laws into variables
20) It would be just -1 over
What I thought was done well was like I said before, that the examples are very simple but they show the learning outcomes clearly. I can understand you explanations really well and if I was a beginner at exponents, I would get a sense of how to do it if I read your learning outcomes.
A few suggestions I would like to point out is to put at least a short sentence when explaining the question, for example #2 had just the example. Maybe for #18 an example like finding the shaded area between 2 squares could make it more detailed. My final suggestion is to put a few pictures for some of the questions like in #3 where you have to show a building model as an example. Overall, I can learn lots on exponents by reading this and it was detailed.
November 15, 2016 at 6:28 am
Thanks Nicholas, Check your OneNote for specific feedback on your post.