Everything I know about exponents: 

---

1. Represent repeated multiplication with exponents

2 · 2 · 2 is the same thing as 2³ because 2³ is the same thing as multiplying 2 by itself three times. Another example would be 4², because it would be the same thing as 4 · 4 and both things would be equal to 16. Using powers is a simpler way to write repeated multiplication.

---

3. Demonstrate the difference between the exponent and the base by building models of a given power, such as 2³  and 3²

This cube is 5 · 5 · 5, which is the same thing as 5³. The base is the thing that is being multiplied, which is 5 and the exponent expresses the amount of times the base is being multiplied by itself, which is 3. To find the volume of a cube, the formula length x width x height must be used. In this case, since it is a cube, the length, width and height are all equal to 5. Therefore, the expression is 5³ and not 3⁵. The picture on the right shows the expression that would be used to find the volume of this cube with the base and exponent labelled.

---

5. Evaluate powers with integral bases (excluding base 0) and whole number exponents.

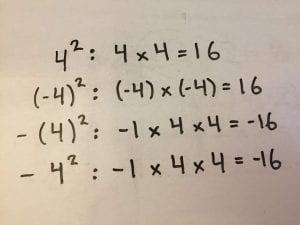
(-4)², -4², -(4)² may look like the same question however, the truth is that you will get different answers for them. For instance, (-4)² written as repeated multiplication would be equal to (-4) x (-4), which equals to 16, while -4² would be -1 · 4 · 4, which equals to -16 because of bedmas, since you would figure out the exponents in the brackets and then add the negative sign. -(4)² would also be equal to -1 · 4 · 4, which would be equal to -16 as well. It is important to recognize the different ways that questions with exponents may be written in order to get the right answer. If the base is positive, the answer will be positive unless there is a negative coefficient. If the base is negative and the exponent is an even integer, then the answer will be positive. If the base is negative and the exponent is an odd integer, then the answer will be negative.

---

7. Explain the exponent laws for multiplying and dividing powers with the same base

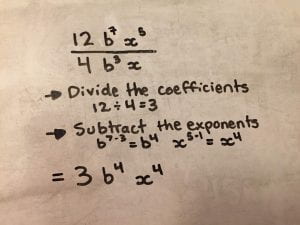
When multiplying a power with the same base, you can use the product law and add the exponents. The opposite to that is division, in which case you would use the quotient law and subtract the exponents. For multiplication, in the first example on the left above, you would convert 4² x 4³ into 4⁵ by adding the exponents together, which would equal to 1024. Another example would be b² x b⁴ converted to b⁶ by using the product law. For division, in the first example on the right above, you would convert b⁵ divided by b³ into b² by subtracting the exponents using the quotient law. On the second example on the left you would use the product law which means that the first step would be to add the exponents. So, 4(n³·n²) · 3(f²·f⁵) would be equal to 4(n³⁺²) · 3(f²⁺⁵) which would be equal to 4(n⁵) · 3(f⁷). The next step would be to multiply the coefficients, so 4·3=12. Therefore, the final answer would be 12 n⁵f⁷. For the second example on the right you would use the quotient law which means that the first step would be to divide the coefficients, which are 12 and 4, so 12 ÷ 4 = 3. The next step would be to subtract the exponents. So, b^7-3 = b⁴ and x^5-1= x⁴. Therefore, the answer would be 3 b⁴ x⁴.

---

9. Explain the law for powers with an exponent of zero.

The law for powers with an exponent of zero is that if the base is ≠ 0, then the power will equal to 1. This rule would apply to both integral and variable bases. In the example on the right, it is shown that the law of powers with an exponent of zero is used for fractions and integral bases. In the example on the left, it is shown that the law for powers with an exponent of zero is used for variable bases. Some examples using integral bases include 2⁰ = 1, 4⁰ = 1 and 274⁰ = 1. Some examples using variable bases include b⁰ = 1, x⁰ = 1 and (x⁴n⁶)⁰ = 1. Some examples with fractions include (2/3)⁰ = 1, (1/5)⁰ = 1 and (-1/4)⁰ = 1. When there is a negative sign inside the brackets, the answer will be positive. When the negative sign is outside of the bracket, the answer will be negative, because the rules of bedmas would be applied: first the things inside the brackets will be solved and then the negative sign will be added to the answer.

 

---

11. Explain the law for powers with negative exponents.

The law for powers with negative exponents is to convert a negative exponent to a positive exponent, you must flip the base making its reciprocal and then evaluate the remainder of the expression by using a positive exponent, since you can’t use negative exponents. In one of the examples above in the left picture, to convert b-⁴ you must turn it into fraction form as (b^-4/1) and then flip the base making its reciprocal and convert the fraction into (1/b⁴). In the example on the right, it is shown that we may also convert fractions with negative exponents to fractions with positive exponents by swapping the numerator and the denominator. For example, (1/4)^-3 is equal to (4/1)³ . Then, to evaluate this expression, you would apply the exponent 3 to both 4 and 1 and the fraction would then be 64/1, which is equal to 64.

---

13. I can apply the exponent laws to powers with both integral and variable bases.

If you already know how to use the exponent laws on integers, then you can easily use them on variables as well. It’s the same. For example, to evaluate m⁶ · m²= m⁸, you would use the exact same steps as if you were to evaluate 2⁶ · 2² = 2⁸. It’s the same thing for the quotient law and the power law. For division, you would use the same steps to evaluate (y⁶/y³) = y³ and (5⁶/5³) = 5³. For the power law, you would use the same steps to get from (x⁴)² = x⁸ just like (4⁴)² = 4⁸. In the example above, I explained the product law using variables in one example and integers in the other one.

---

15. Use the order of operations on expressions with powers.

Sometimes while evaluating expressions with powers, we may forget about bedmas because of all the exponent laws we need to apply, however, it is still as important as it is when evaluating addition, subtraction, multiplication and division. I would say that one of the most common errors when it comes to forgetting orders of operations is remembering to do brackets first, because we can sometimes forget to do them first when we need to think about and apply all the applicable exponent laws. In the example in the right, the first step to evaluating this expression would evaluating the things in the brackets first, which would mean that you would apply the exponent to every number in the brackets. For example, (4 x³y) ² would be equal to (4²x⁶y²), (5xy³)⁴ would be equal to (5⁴x⁴y¹²) and (10x²y)³ would be equal to (10³x⁶y³). Then, you would apply the exponents to the integral bases, which would mean that (4²x⁶y²) would be (16x⁶y²), (5⁴x⁴y¹²) would be (625x⁴y¹²) and (10³x⁶y³) would be (1000x⁶y³). Then, you would use the exponent laws and apply the product law first. You would multiply 16 · 625 and add x⁶⁺⁴ and y²⁺¹² for the numerator and you would leave the denominator as it is because there’s nothing you can multiply it by. This would result in the numerator being 10 000 x¹⁰y¹⁴ and the denominator staying 1000x⁶y³. Then, you would apply the quotient law and divide the coefficients and subtract the exponents. So, 10 000 divided by 1000 = 10, x^{10 – 6} = x⁴ and y^{14 – 3} = y¹¹. Therefore, the answer would be 10 x⁴y¹¹.

---

17. Identify the error in applying the order of operations in an incorrect solution.

While evaluating an expression containing powers, it can sometimes get confusing when you have to remember the order of operations, as well as the exponent laws. Because of this, you sometimes make mistakes. It’s important to remember the order of operations, which is Brackets, Exponents, Division, Multiplication, Addition and Subtraction. In the example equation above, the solution on the left is wrong, because instead of dividing 64 by 4 and then adding 4, which is the proper way to evaluate the expression using bedmas, 4 and 64 were added together and the result was divided by 4. The picture on the right shows the right solution, because 64 was divided by 4 and the quotient was then added to 4.

---

19. Use powers to solve problems (growth problems)

Word problem: The speed of the wind in New York city doubles every hour. Right now, the speed is 3 km per hour. How many km per hour will the wind speeds be in the following amounts of time?

Powers can be used to evaluate numerous word problems and expressions, including growth problems. In the example word problem that I created, for every hour the previous speed of the wind must be doubled, meaning that it is being multiplied by 2 or having 100% of the previous amount added onto it. In this case, I made a chart to indicate the wind speed. As shown in the picture, you may also write a formula in order to help you evaluate the wind speed per hour at a specific hour. For example, for the first hour, you would write 3 · 2¹, because the starting wind speed was 3 and for each hour, the amount doubles. Therefore, in the formula, the 3 represents the starting wind speed, the 2 represents that the wind speed doubles every hour and the exponent represents the number of hours.

Anna’a post

Math Core Competency Reflection