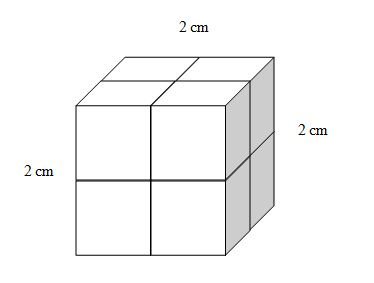
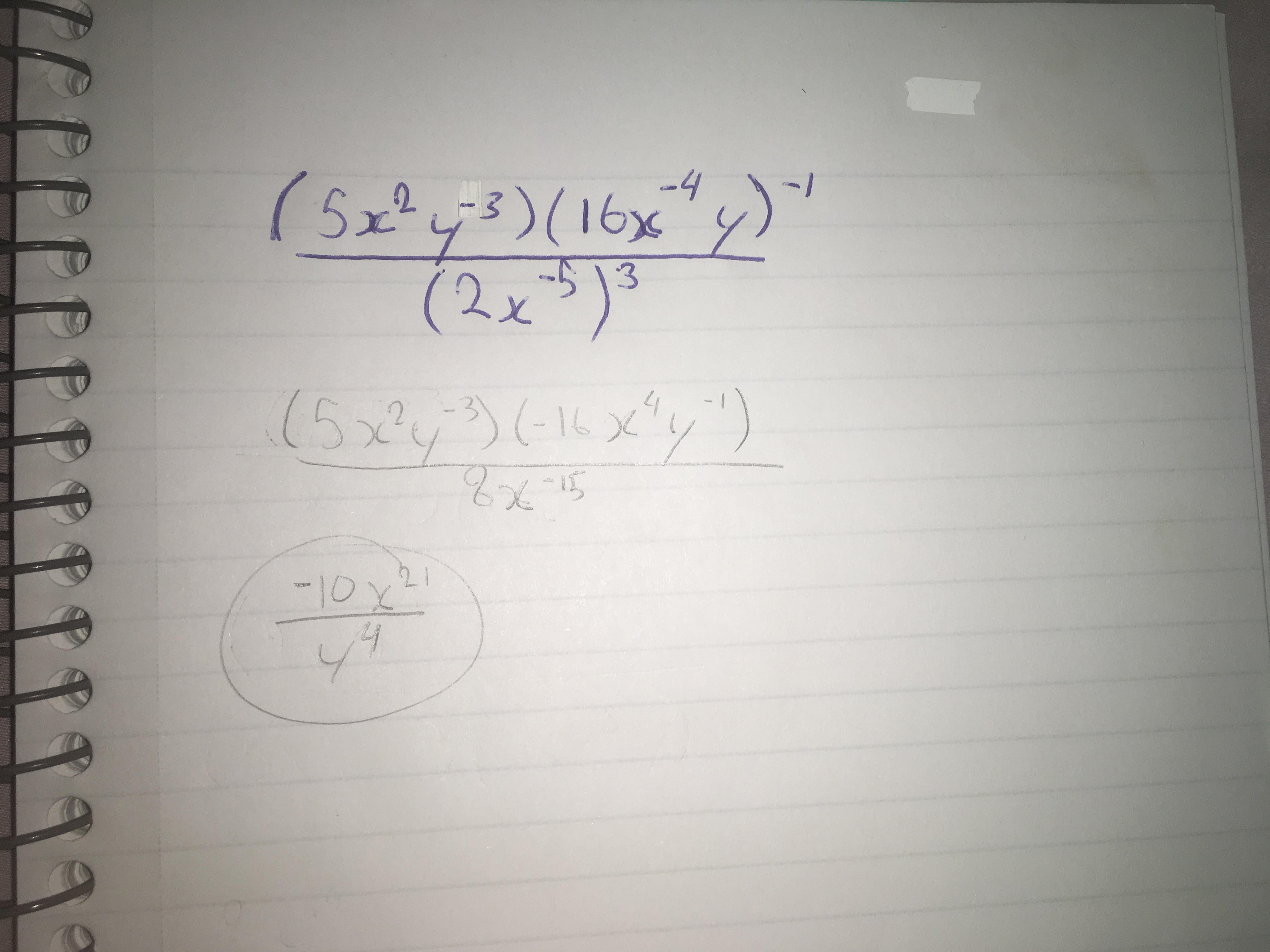Alternative assignment to peer tutoring
Linear relations
Video 1: https://youtu.be/1xfbBHE3UCA
In this video it is explaining how you can take an increasing or decreasing patteren and put it into a chart, representing a constant change in the independnt and dependant variable. They are showing you how you can take constant patterned information, chart it and turn it into an expression which you can then follow to continue the pattern. For example they use the relation between the distance a car is going and the cost of gas per that distance.
Video 2: https://youtu.be/MweKCXkZ1GA
This video is similar to the last video but it has more of an explanation of y=mx+b and he explains more about what each part of that expression represents. M=slope b=y-intercept. He also explains what that means into further detail as if you were learning linear relations for the first time. He does more exmples with finding x and y and graphing it rather than charting it using different examples with different variables.
Linear equations and innequalities
Video 1: https://youtu.be/bAerID24QJ0
This video starts off by demonstrating how isolate x/find x in a simple linear equation. He also shows you how to deal with an equation if it is involving fractions, he shows you that expressing linear equations with fractions is the same thing but you multiply by the reciprocal to isolate the variable. He also demonstrates how you can check your final answer by substituting x.
Video 2: https://youtu.be/0X-bMeIN53I
This video is based on linear inequalities, he first explains what a linear inequality is. Then he tell you a very important rule, that when dividing by a negative number you must flip the inequality. He then gives an example of what that means. Throughout the video he goes on explaining more concepts and steps, he then demonstrates examples. Unfortunatley he does not explain the 3 steps of checking your answer, his video is more based on making sure you know the rule of flipping the sign and examples being demonstrated and solved.
Scale factor and similarity
Video 1: https://youtu.be/XtkU4VkWh8I
He begins with defining what scale factor is, he then demonstrates how to calculate it and how to use it. He explains all of the terminology he uses to a better, simple understanding. He first changes the values so that they are in the same units, then compares the larger image to the smaller image, he demonstrates how to fin =d the scale factor by comparing the values of one object to the other. He demonstrates cross multiplication to find the unknown length.
Video 2: https://youtu.be/FmZ2sKDb2SI
This video is only 1 of 8 on this topic, but he begines by explaning what similarity is. He explains that with similarity the corresponding angles are equal and that the corresponding sides are in proportion. He then demonstrates examples in order to explain what that means. He explains that the objective of similarity is to find the scale factor. He shows how to use scale factor to find side “x” based on similarity. He also explains cross mutiplication to find the missing length of an object
Hubbard2017DAReflections
After reading the first article it made me realize how dangerous social media really is. There are lots of fake accounts out there that are being used for various things, and alot of people tend to believe whatever they read on the internet. After reading this article i will definitly try and be more careful and not believe every single thing i see or read off of the internet because there is a possibility it could be a scam, it made me more aware of how social medias can affect a person or multiple people if they are targeted by it.
the second link has given me a reminder that alot of information on the internet is fake or not 100% true and that if i wan’t to believe that something is 100% true, then i should research more about the topic and see if i get the same results on more than one website. Also i really dont like the fact that people had posted tragedies that were made up to get a form of attention.
Both of these links have a large affect of me because social medias are a big part of my life and generation and to think that i cannot rely on something so big puts an impact on me because then i think well what’s the point of social medias then?
Statistics
statistics play a large role in our society, the role of statistics is used in many ways and can affect the way we make decisions. It is a way of having a source of knowledge on whether we could do one thing or another. For example if you were to move to a city, the crime rates and average house costs would help your decision. Statistics can also be used in something as simple as at McDonalds, whether the company is going to keep a certain meal based on the averages of costumer likes and dislikes on the product. Statistics are a way of simplifying knowledge on the topic so that the information and facts can be read easier.
After reading this article i have learned more about the importance of the role of statistics in our society such as in general information or more in depth topics. Statistics are invloved in most of the things that take apart in our decisions in our everyday life. Whatever buisnesses, textbooks, people and especially the internet tell you, it’s all based on statistcs. However statistics cannot always be 100% reliable and can be made up easily. There can be bad sampeling, misleading statistics or even unfair poll questions that can be minipulated by the asker in order to get the answer they are looking for. Therefore statistics are not always reliable and we should not let them fully take over our decisions, we should take some time to analyze everythng ourselves so we can have a better understanding and see if what other people are saying actually makes sense.
Everything i know about exponents
1: represent repeated multiplication with exponents:
An example of repeated multplication would be writing/expanding out as (2)(2)(2)(2) or 2x2x2x2 or 2•2•2•2
2. Describe how powers represent repeated multplication:
Poweres represent repeated multiplication by showing that ex. (5)(5)(5)(5) would be written as because it’s saying multiply 5 by 5, 4 times. The exponent is 4 because thats how many times your multiplying the base, which is 5. The exponent is the small number and the base is the larger number. So
= (5)(5)(5)(5)
3. Demonstrate the difference between the exponent and the base:
in a power, there’s an exponent and a base, a little number and a larger number. The little number is the exponent and the larger number is the base. The base is multiplied by itself as many times as the exponent. So if the base is 5 and the exponent is 3, then 5 multiplies by itself 3 times. (5)(5)(5) =
4. Demonstrate the difference between two givin powers in which the exponent and the base are interchanged by using repeated multiplication:
=
so this means that is different than
.
means you multiply 2 by itself 3 times, so, (2)(2)(2) because the base is 2, and the exponent is 3, and you multiply the base by itself as many times as the exponent tells you to.
means multiply 3 by itself twice. So (3)(3) so these are two completely different answers.
= 8 and
= 9. They do not equal the same answer even though they both use the same numbers.
5. Evaluate powers with integral bases (excluding base 0) and whole number exponents:
ex. = 125
ex. = 81
ex. = 32
6. Explain the role of parentheses in powers by evaluating a given set of numbers such as ,
and
:
so means (-2)(-2)(-2)(-2) = +16
means (-1)(2)(2)(2)(2) = (-16)
means (-1)(2)(2)(2)(2) = (-16)
7.explain the exponent law for multiplying and dividing powers with the same base:
law for dividing: ex. , you would subtract the exponents while keeping the base as it is so it becomes
wich equals to
= 16
law for multiplying: ex. , you would add the exponents while keeping the base as it is so it becomes
which equals to
= 32
8. Explain the exponent laws for raising a product and quotient to an exponent:
raising product to an exponent would be you would multiply the exponents, you multiply because like any other equation, if there’s a bracketed number next to another number it means multiply ex. 2(5) just means 2×5 = 10. And you multiply the exponents because it follows pemdas or bedmas.so..
=
=
= 15,625
raising quotient to an exponent is the same as dividing same base powers, you subtract the exponents. So over
=
=
= 25
9. Explain the law for powers with an exponent of 0:
anything to the power of 0 = 1
10. Use patterns to show that a power with an exponent of zero is equal to one:
When the power decreases, the answer divides by it’s base. Ex = 32
, to find the answer you can take 32 from
And divide it by the base to get the answer for
= 16 this means you would divide 32 by 2(base) to get 16
same with to get the answer you can divide 16 by 2 = 8
= 8
= 8/2 = 4.
= 4
= 4/2 = 2.
= 2
then to get , you continue on the rule, you find the answer for
Which is 2 and divide it by the base which is 2 in this case. So
= 2/2 = 1.
= 1
11. Explain the law for powers with negative exponents:
the law for negative exponents is the same for any base except zero. If the base is raised to a negative exponent, you must reciprocal the base so then the exponent becomes positive. Ex. over 5, you would change it so 5 is now over 2, which makes the exponents positive. Then you complete the equation, in this case you would do
= 25. Then divide the numerator by the the denominator so 25/2=12.5
12. Use patterns to explain the negative exponent law:
For example you would reciprocal the base. It becomes
over 2, then you just solve it how you normally would. It becomes 1 over 3 because before, it was just 3 and 3=3 over 1
13.
I can apply the exponent laws to powers with both inegral and variable bases:
when solving powers with variables as bases, you always follow the same rules as if the base were a number but you may not be able to solve the equation completely
ex. =
there is no different ce between the power and the answer because it can’t be solved any further.
ex. x
=
This is the final answer because you can’t multiply Y by itself 7 times and get an answer further than this answer.
ex. divided by
=
This is the final answer because you can’t multiply N by itself twice and get an sneer further than this answer.
14. I can identify the error in a simplification of an expression involving powers:
I will spot the error in the equation below and correct it-
=
this answer is wrong.
=
=
15. Use order of operations on expressions with powers:
when following the order of operations with powers, we always use bedmas.
ex. x
= 2x2x2x2 = 16, 4x4x4 = 64, 16×64=1024
Ex. 2 =
= 4×4= 16. 2×16= 32
16. Determine the sum and difference of two powers:
adding powers ex. = (4x4x4) + (2x2x2x2x2) = 64+32= 96
subtracting powers ex. = (3x3x3) – (6×6) = 27-36= -9
17. Identify the error in applying the order of operations in an incorrect solution:
3 =
this is wrong because with order of operations, you always do the exponent before you multiply.
3 = 6x6x6 = 216. 216 x 3 = 648
18. Use powers to solve measurement problems:
Imagine a shaded square with each side 5cm, and a smaller, white square with each side 2cm sitting inside the shaded square. how do you find the area of the shaded part? Well Area=LxW, because we are talking about perfect squares, LxW is the same as saying To the power of 2. for the larger square so = 25. Then the smaller white square,
= 4. So to find the shaded part you subtract them, 25- 4 = 21. Area of the shaded part =
19. Use powers to solve growth problems:
Ex. There are 20 people at a concert. The amount of people doubles ech hour, how any people will there be in ____ hours?
2 hours?
20 x = 20 x 4= 80 people. In 2 hours there will be 80 people
4 hours?
20 x = 20 x 16 = 320 people in 4 hours
6 hours?
20 x = 20 x 64 = 1280 people in 6 hours
etc.
20. Applying the order of operations on expressions with powers involving negative exponents and variable bases:
A power involving a variable base with a negative exponent would be:
LateX coding
Example 1: exponent:
Example 2: two digit exponent:
example 3: fractions
example 4: adding operations:
Example 5: change size:
Example 6: change text color
Example 7: change background color: